Page 68 - 2024年第55卷第8期

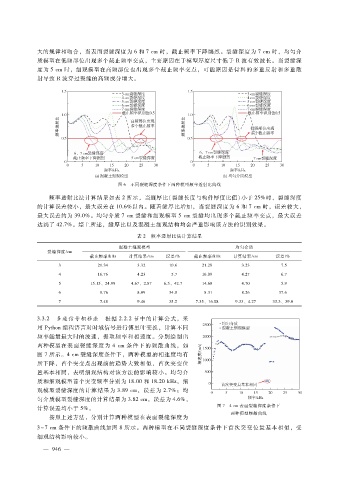
大的规律相吻合，当表面裂缝深度为 ６和 ７ｃｍ时，截止频率下降剧烈。裂缝深度为 ７ｃｍ时，均匀介
质模型在低频部位出现多个截止频率交点，主要原因在于模型厚度尺寸低于 Ｒ波有效波长。当裂缝深
度为 ５ｃｍ时，细观模型在高频部位也出现多个截止频率交点，可能原因是骨料的多重反射和多重散
射导致 Ｒ波穿过裂缝的高频成分增大。

图 ６ 不同裂缝深度条件下两种模型频率透射比曲线

频率透射比法计算结果如表 ２所示，当缝厚比（裂缝长度与构件厚度比值）小于 ２５％时，裂缝深度
的计算误差较小，最大误差在 １０．６％以内。随着缝厚比增加，当裂缝深度为 ６和 ７ｃｍ时，误差较大，
最大误差约为 ３９．０％。均匀介质 ７ｃｍ裂缝和细观模型 ５ｃｍ裂缝均出现多个截止频率交点，最大误差
达到了 ４２．７％。综上所述，缝厚比以及混凝土细观结构均会严重影响该方法的识别效果。
表 ２ 频率透射比法计算结果

混凝土细观模型 均匀介质
裂缝深度?ｃｍ
截止频率?ｋＨｚ 计算结果?ｃｍ 误差?％ 截止频率?ｋＨｚ 计算结果?ｃｍ 误差?％
３ ２１．３４ ３．３２ １０．６ ２１．２８ ３．２３ ７．５
４ １６．７６ ４．２３ ５．７ １６．０９ ４．２７ ６．７
５ １５．１５ 、２４．９９ ４．６７、２．８７ ６．５、４２．７ １４．６０ ４．７０ ５．９
６ ８．７６ ８．０９ ３４．８ ８．３１ ８．２６ ３７．６
７ ７．４８ ９．４６ ３５．２ ７．３５ 、１６．０８ ９．３３、４．２７ ３３．３、３９．０

３．３．２ 多道信号相移法 根据 ２．２．２节中的计算公式，采
用 Ｐｙｔｈｏｎ编程语言对时域信号进行傅里叶变换，计算不同
频率能量最大时的波速，提取频率和相速度。分别绘制出
两种模型在表面裂缝深度为 ４ｃｍ条件下的频散曲线，如
图 ７所示。４ｃｍ裂缝深度条件下，两种模型的相速度均有
所下降，首个突变点出现前的趋势大致相似，首次突变位
置基本相同，表明细观结构对该方法的影响较小。均匀介
质和细观模型首个突变频率分别为 １８．００和 １８．２０ｋＨｚ，细
观模型裂缝深度的计算结果为 ３．８９ｃｍ，误差为 ２．７％；均
匀介质模型裂缝深度的计算结果为 ３．８２ｃｍ，误差为 ４．６％，
图 ７ ４ｃｍ表面裂缝深度条件下
计算误差均小于 ５％。
两种模型频散曲线
按照上述方法，分别计算两种模型在表面裂缝深度为
３～７ｃｍ条件下的频散曲线如图 ８所示。两种模型在不同裂缝深度条件下首次突变位置基本相似，受
细观结构影响较小。

６
— ９ ４ —