Page 69 - 2024年第55卷第8期
P. 69
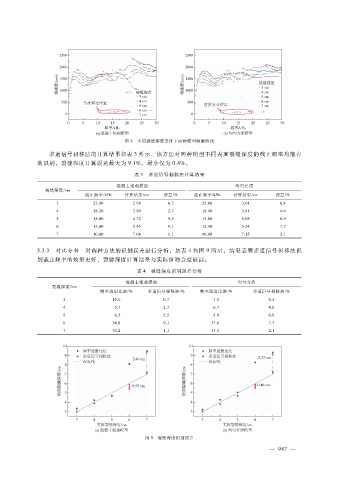
图 8 不同裂缝深度条件下两种模型频散曲线
多道信号相移法的计算结果如表 3所示,该方法对两种模型不同表面裂缝深度的截止频率均能有
效识别,裂缝深度计算误差最大为 9.1%,最小仅为 0.4%。
表 3 多道信号相移法计算结果
混凝土细观模型 均匀介质
裂缝深度?cm
截止频率?kHz 计算结果?cm 误差?% 截止频率?kHz 计算结果?cm 误差?%
3 23.80 2.98 0.7 22.80 3.01 0.4
4 18.20 3.89 2.7 18.00 3.81 4.6
5 15.00 4.72 5.5 13.60 5.05 0.9
6 13.00 5.45 9.1 12.40 5.54 7.7
7 10.00 7.08 1.1 96.00 7.15 2.1
3.3.3 对比分析 对两种方法的识别误差进行分析,如表 4和图 9所示,结果表明多道信号相移法识
别截止频率的效果更好,裂缝深度计算结果与实际值吻合度较高。
表 4 裂缝深度识别误差分析
混凝土细观模型 均匀介质
裂缝深度?cm
频率透射比法?% 多道信号相移法?% 频率透射比法?% 多道信号相移法?%
3 10.6 0.7 7.5 0.4
4 5.7 2.7 6.7 4.6
5 6.5 5.5 5.9 0.9
6 34.8 9.1 37.6 7.7
7 35.2 1.1 33.3 2.1
图 9 裂缝深度识别误差
— 9 4 7 —