Page 67 - 2024年第55卷第8期

３．３ 检测方法分析及验证 以 ４ｃｍ表面裂缝深度缺陷为例，分别采用频率透射比和多道信号相移法
识别均匀介质和混凝土细观模型的截止频率，研究两种方法的检测机理和识别效果。
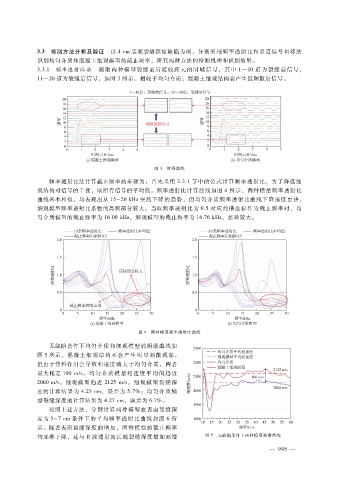
３．３．１ 频率透射比法 提取两种模型裂缝前后接收阵元的时域信号，其中 １—１０道为裂缝前信号，
１１—２０道为裂缝后信号，如图 ３所示。相较于均匀介质，混凝土细观结构会产生低频散射信号。

图 ３ 时程曲线

频率透射比法计算截止频率的步骤为：首先采用 ２．２．１节中的公式计算频率透射比，为了降低细
观结构对信号的干扰，取所有信号的平均值。频率透射比计算曲线如图 ４所示，两种模型频率透射比
曲线基本相似，均表现出从 １５～２０ｋＨｚ突然下降的趋势，但均匀介质频率透射比曲线下降速度更快，
细观模型频率透射比系数的高频部分较大。当取频率透射比为 ０．５对应的横坐标作为截止频率时，均
匀介质模型的截止频率为 １６．０９ｋＨｚ，细观模型的截止频率为 １６．７６ｋＨｚ，差异较大。

图 ４ 两种模型频率透射比曲线

无缺陷条件下均匀介质和细观模型的频散曲线如
图 ５所示。混凝土细观结构不 会产生 明显 频散现 象，
但由于骨料作用会导致相速度略大于均匀介质，两者
最大相差 １００ｍ?ｓ，均匀介质 模型 相速 度平 均值趋近
２０６０ｍ?ｓ，细观模型趋近 ２１２５ｍ?ｓ。细观模型裂缝深
度的计算结果为 ４．２３ｃｍ，误差为 ５．７％；均匀介质模
型裂缝深度的计算结果为 ４．２７ｃｍ，误差为 ６．７％。
按照上述方法，分别计算两种模型在表面裂缝深
度为 ３～７ｃｍ条件下的平均频率透射比曲线如图 ６所
示。随着表面裂缝深度的增加，两种模型的截止频率
均逐渐下降，这与 Ｒ波透射波长随裂缝深度增加而增 图 ５ 无缺陷条件下两种模型频散曲线

— ９ ４ ５ —