Page 77 - 2024年第55卷第10期

（１）当应变为 ｘ ≤１时，由式（１３）（１５）（２６）和式（２４）得

２ｆ ｆ ２ｘ ｘ
４
３
ｃ
ｃ
２
ｍ ＝ ｘ － ∫ [ ａｘ＋ （３ － ２ａ） ＋ （ａ－ ２ ） ] （２７）
ｙｄｘ＝ ｘ －
１
槡 ０ 槡 ０ ３ ２
１
１
２
λ Ｅε ｃｐ
λ Ｅε ｃｐ
ｐ
ε＝ ｍ ε ｃｐ
由此得 珔 ｃ ２ 。根据式（２６）得损伤演化方程
２
３
ｆ ｙ ｆ ａｘ ＋ （３ － ２ａ）ｘ＋ （ａ－ ２）ｘ
ｃ
１
１
１
ｃ
ｄ＝ １ － ＝ １ － （２８）
ｃ
０ ２ ０ ２
Ｅε ｃｐ ｘ － ｍ Ｅε ｃｐ ｘ － ｍ
（ ２）当应变为 ｘ＞１时，由式（１３）（１５）（２６）和式（２４）（２５）得

ｆ ６ ＋ ａ １ ２（２ａ－ １ ） （ｘ － １ ） ４ａ－ １
槡
ｃ
２
２
ｍ ＝ ｘ － ６ { １ ＋ ｌｎ［ａ（ｘ － １ ）＋ ｘ］ ＋ ２ ａｒｃｔａｎ ｘ ＋ １ } （２９）
２ ａ ２
槡 ０ ２ ａ ４ａ－ １
槡
λ Ｅε ｃｐ
２
２
ｐ
由此得 珔 ｃ ２ 。根据式（２５）（２６）得损伤演化方程
ε＝ ｍ ε ｃｐ
ｆ ｙ ｆ １ ｘ
ｃ
ｃ
ｄ＝ １ － ＝ １ － （３０）
ｃ ２
Ｅε ｃｐ ｘ － ｍ Ｅε ｃｐ ｘ － ｍ ａ（ｘ － １）＋ ｘ
０ ２ ０ ２ ２
－ ６
＝ １４７０ × １０ ，ａ ＝
算例：强度等级 Ｃ３０的水工混凝土轴心抗压强度标准值为 ｆ＝ ２０．１ＭＰａ ，ε ｃｐ
ｃ １
２．１５，ａ＝ ０．７４ 。受压损伤的分析过程如下：
２
ｆ
ｄ σ ｃ ｃ ２０．１
６
根据式（ ２４），初始弹模为 Ｅ ＝ ＝ ａ ＝ ２ ．１５ × ＝ ０．０２９４ × １０ ＭＰａ。
０ １ － ６
ｄ ε ｃ ε ｃ ＝ ０ ε ｃｐ １４７０ × １０
当 ｘ ≤１时，ｙ按式（２４）计算，ｍ 按式（２７）计算，ｄ按（２８）计算；当 ｘ＞１时，ｙ按式（２５）计算，
ｃ
２
ｍ 按式（２９）计算，ｄ按式（３０）计算。根据文献［３３］，混凝土压缩试验曲线的 λ值在 １．４２８７～１．８６７４之
２ ｃ
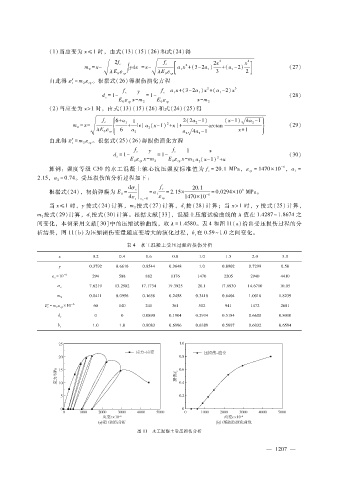
间变化，本例采用文献［３０］中的压缩试验曲线，取 λ ＝ １．４５８０。表 ４和图 １１（ａ）给出受压损伤过程的分
析结果，图 １１（ｂ）为压缩损伤变量随应变增大的演化过程，ｂ在 ０．５９～１．０之间变化。
ｃ
表 ４ 水工混凝土受压过程的损伤分析
ｘ ０．２ ０．４ ０．６ ０．８ １．０ １．５ ２．０ ３．０
ｙ ０．３７９２ ０．６６１６ ０．８５４４ ０．９６４８ １．０ ０．８９０２ ０．７２９９ ０．５０
ε ｃ １０ － ６ ２９４ ５８８ ８８２ １１７６ １４７０ ２２０５ ２９４０ ４４１０
×
７．６２１９ １３．２９８２ １７．１７３４ １９．３９２５ ２０．１ １７．８９３０ １４．６７１０ １０．０５
σ ｃ
０．０４１１ ０．０９５６ ０．１６３８ ０．２４５８ ０．３４１８ ０．６４０４ １．００１６ １．８２３９
ｍ ２
ｐ
ε ＝ × － ６ ６０ １４０ ２４１ ３６１ ５０２ ９４１ １４７２ ２６８１
珔 ｃ ｍ ２ ε ｃｐ １０
０ ０ ０．０８９０ ０．１９０４ ０．２９３４ ０．５１８４ ０．６６００ ０．８０１０
ｄ ｃ
１．０ １．０ ０．８０８３ ０．６９９６ ０．６３８９ ０．５８９７ ０．６０３２ ０．６５９４
ｂ ｃ
图 １１ 水工混凝土受压损伤分析
２
— １ ０ ７ —