Page 73 - 2024年第55卷第10期
P. 73
顶部施加,单元底部 节点 采用 法 向 固 定 约 束,底 部 一 角 点 采 用 三 向 链 杆 的 固 定 约 束,以 商 业 软 件
ABAQUS进行数值计算,所用的单元类型为 C3D8R八节点六面体单元。混凝土材料采用 CDP模型,
根据实际试件的混凝土材料特性,选用的计算参数见表 1。
表 1 混凝土数值模拟计算的力学参数 [30 - 31]
弹性模量 泊松比 剪胀角 Ψ 偏心率 应力比 抗拉强度 f 抗压强度 f 断裂能 G f
c
t
材料参数 K c
?GPa v ?(°) η σ σ ?MPa ?MPa ?(N?m)
珚 cc ? 珚 c
单向拉伸循环 30.5 0.2 30 0.1 0.667 1.16 3.5 40 55
单向压缩循环 30 0.2 30 0.1 0.667 1.16 2.8 28 200
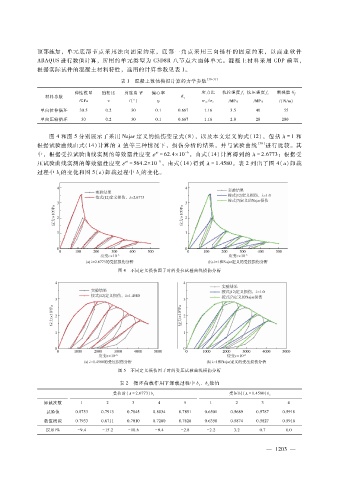
图 4和图 5分别展示了采用 Najar定义的损伤变量式(8),以及本文定义的式(12),包括 λ = 1和
根据试验曲线由式( 14)计算的 λ值等三种情况下,损伤分析的结果,并与试验曲线 [30] 进行比较。其
- 6
pt
ε
中,根据受拉试验曲线实测的等效塑性应变 珔 = 62.4 × 10 ,由式(14)计算得到的 λ = 2.6773 ;根据受
pt
- 6
压试验曲线实测的等效塑性应变 珔 = 564.2 × 10 ,由式(14)得到 λ = 1.4580。表 2列出了图 4(a)卸载
ε
过程中 b的变化和图 5(a)卸载过程中 b的变化。
c
t
图 4 不同定义损伤因子时的受拉试验曲线损伤分析
图 5 不同定义损伤因子时的受压试验曲线损伤分析
表 2 循环荷载作用下卸载过程中 b、b数值
t c
受拉时( λ = 2.6773)b t 受压时( λ = 1.4580)b c
卸载次数 1 2 3 4 5 1 2 3 4
试验值 0.8753 0.7913 0.7845 0.8034 0.7851 0.6501 0.5689 0.5787 0.5918
数值模拟 0.7933 0.6711 0.7010 0.7280 0.7628 0.6358 0.5874 0.5827 0.5916
误差?% - 9.4 - 15.2 - 10.6 - 9.4 - 2.8 - 2.2 3.2 0.7 0.0
2
— 1 0 3 —