Page 76 - 2024年第55卷第10期

根据式（２１）得损伤演化方程
ｙ ｍ － ｘ
ｄ＝ １ － ＝ １ － （２３）
ｔ
ｘ － ｍ １ （ｍ － １ ）（ｘ － ｍ ）
１
＝
算例：强度等级为 Ｃ３０的水工混凝土轴心抗拉强度标准值为 ｆ ＝ ２．０１ＭＰａ，Ｅ ＝ ３００００ＭＰａ，则 ε ｔｐ
ｔ ０
－ ６
ｆ?Ｅ ＝ ２．０１?３００００ ＝ ６７ × １０ 。如果有通过试验获得的应力－ 应变全曲线，则根据全曲线确定 ｍ，以及由
ｔ
０
ｐｔ
第一次卸载点的 珔 按式（１４）计算损伤耗能修正系数 λ ，进行损伤分析。如无试验曲线，可参考他人的
ε
试验成果，确定 λ值。参照图 ４，本算例假定 ｍ＝ ４，ｘ ＝ １．２时开始第一次卸载。λ采用由第 ４节试
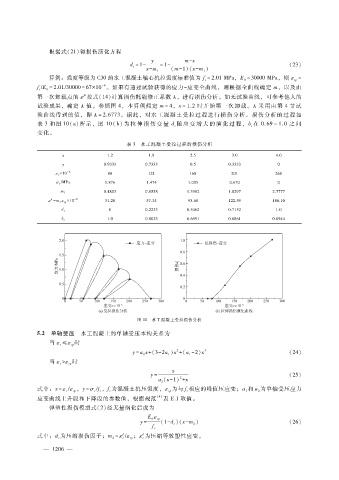
验曲线得到的值，即 λ ＝ ２．６７７３ 。据此，对水工混凝土受拉过程进行损伤分析。损伤分析的过程如
表 ３和图 １０（ａ）所示，图 １０（ｂ）为 拉 伸 损 伤 变 量 ｄ随 应 变 增 大 的 演 化 过 程，ｂ在 ０．６９～１．０之 间
ｔ
ｔ
变化。
表 ３ 水工混凝土受拉过程的损伤分析
ｘ １．２ １．８ ２．５ ３．０ ４．０
ｙ ０．９３３３ ０．７３３３ ０．５ ０．３３３３ ０
×
ε ｔ １０ － ６ ８０ １２１ １６８ ２０１ ２６８
σ ｔ ?ＭＰａ １．８７６ １．４７４ １．００５ ０．６７０ ０
０．４８０３ ０．８５５８ １．３９８２ １．８２９７ ２．７７７７
ｍ １
ｐ
×
珔 ＝ ｍ １ ε ｔｐ １０ － ６ ３１．２８ ５７．３４ ９３．６８ １２２．５９ １８６．１０
ε
０ ０．２２３３ ０．５４６２ ０．７１５２ １．０
ｄ ｔ
１．０ ０．８０２３ ０．６９９１ ０．６８６１ ０．６９４４
ｂ ｔ

图 １０ 水工混凝土受拉损伤分析

５．２ 单轴受压 水工混凝土的单轴受压本构关系为
时
当 ε ｃ ≤ε ｃｐ
３
２
ｙ ＝ ａｘ ＋ （３ － ２ａ）ｘ＋ （ａ－ ２ ）ｘ （２４）
１
１
１
＞ 时
当 ε ｃ ε ｃｐ
ｘ
ｙ ＝ （２５）
２
ａ（ｘ － １ ）＋ ｘ
２
为与 ｆ相应的峰值压应变；ａ和 ａ为单轴受压应力
? ，ｙ ＝ σ ｃ ｃ
式中：ｘ ＝ ε ｃ ε ｃｐ ?ｆ，ｆ为混凝土抗压强度，ε ｃｐ ｃ １ ２
ｃ
应变曲线上升段和下降段的参数值，根据规范 ［４］ 表 Ｅ．１取值。
弹塑性损伤模型式（２）经无量纲化后成为
０
Ｅε ｃｐ
ｙ ＝ （１ － ｄ）（ｘ － ｍ ） （２６）
２
ｃ
ｆ
ｃ
ｐ
ｐ
２ ε? ；ε为压缩等效塑性应变。
式中：ｄ为压缩损伤因子；ｍ ＝ 珔 ｃ ε ｃｐ 珔 ｃ
ｃ
— １ ２ ６ —
０