Page 74 - 2024年第55卷第10期

由图 ４—５可知，根据试验曲线确定损伤耗能修正系数 λ ，再按式（１２）的能量公式定义损伤因子
进行计算的损伤数值模拟结果，与试验曲线吻合得最好；吻合较差的是与 Ｎａｊａｒ定义的损伤变量式（８）
相应的损伤分析结果；吻合程度最差的是不考虑其他耗散能 Ｕ 的损伤分析结果。表 ２显示混凝土试
ｄ ２
件在循环荷载作用下实测的 ｂ值在 ０．７８４５～０．８７５３之间变化，ｂ值在 ０．５６８９～０．６５０１之间变化。数值模
ｔ ｃ
拟结果与试验值比较接近，误差为－ １５．２％～３．２％之间。无论是试验值还是计算值，均与 Ｂｉｒｔｅｌ等 ［１９］ 建
议的固定值 ｂ＝ ０．１ 和ｂ＝ ０．７ 有比较大的差别。
ｔ
ｃ
［３２］
为了进一步说明本文方法的正确性，对 Ｒｅｉｎｈａｒｄｔ 的混凝土准静态加载试验进行模拟。试验采
用尺寸 ２５０ｍｍ × ２２０ｍｍ × ５０ｍｍ的混凝土棱柱体试件，试件两侧沿厚度方向各预制 ５ｍｍ × ２０ｍｍ的切
口，作为开裂的起始部位。试件的几何尺寸如图 ６（ａ）所示。混凝土弹性模量 Ｅ ＝ ３９．３ＧＰａ，单轴抗压
０
强度（１５０ｍｍ立方体）ｆ ＝ ４７．１ＭＰａ，单轴抗拉强度 ｆ ＝ ３．８ＭＰａ，断裂能 Ｇ＝ １３２Ｎ?ｍ。试验加载采用
ｃ ｔ ｆ
位移控制，最终在预制切口断面处拉断。针对该试验，采用式（ １６）的损伤变量模型，以及与图 ４受拉
试验曲线相应的 λ值，应用 ＡＢＡＱＵＳ商业软件进行非线性有限元数值模拟，数值模型的有限元网格如
图 ６（ｂ）所示，单元类型为四节点平面应力四边形（ＣＰＳ４Ｒ）单元，共有 ２１９２个单元。底面为固定边
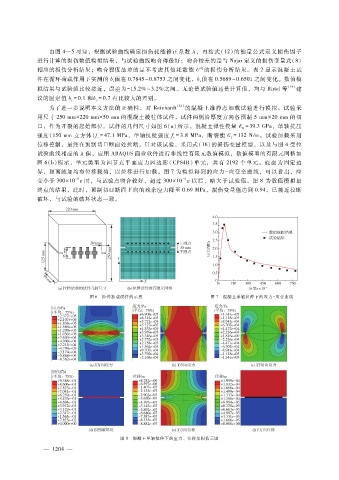
界，顶面施加均布位移载荷，以位移进行加载。图 ７为模拟得到的应力 － 应变全曲线，可以看出，应
－ ６
－ ６
变小于 ３００ × １０ ε 时，与试验点吻合较好，超过 ３００ × １０ ε以后，略大于试验值。图 ８为数值模拟最
终点的结果，此时，预制切口断面 Ｙ向的残余应力降至 ０．６９ＭＰａ，损伤变量值达到 ０．９４，已接近拉断
破坏，与试验的破坏状态一致。

图 ６ 拉伸加载试件的示意 图 ７ 混凝土单轴拉伸下的应力－ 应变曲线

图 ８ 混凝土单轴拉伸下的应力、位移及损伤云图
— １ ２ ４ —
０