Page 70 - 2024年第55卷第10期

比值 ｂ为 ０．７。然而，这一固定的取值与实际不符，混凝土循环加卸载试验曲线显示，这一比值随着
ｃ
循环次数的增加而变化，而非固定值。
混凝土损伤破坏的实质是能量的转化。由热力学定律可知，能量耗散是混凝土变形破坏的本质属
性，它反映了混凝土内部微缺陷的不断发展，强度不断弱化并最终丧失的过程。因此，以能量研究岩
体和混凝土等准脆性材料的破坏是一条可行的途径 ［２０ － ２３］ 。一些学者直接从能量的角度定义损伤变量。
丁发兴等 ［２４］ 同时以弹性模量和能量定义损伤变量，通过两者相等建立了单轴应力状态下混凝土损伤演
化方程和损伤本构模型。Ｋｒａｊｃｉｎｏｖｉｃ等 ［２５］ 、李淑春等 ［２６］ 、任梦宁 ［２７］ 、彭刚等 ［２８ － ２９］ 用 Ｎａｊａｒ能量法来
定义损伤变量。该方法原理清晰，但其定义的损伤变量演化与混凝土实际受压的破坏过程并不十分吻
合。而且，即使材料完全破坏，损伤变量值也不能到达 １．０。
以上学者均将全部耗散能用于定义损伤，本文认为总耗散能并非全部由损伤引起的，而是由两部
分组成：一部分是导致混凝土损伤的耗散能；另一部分是混凝土受外荷载作用时功 － 能转化过程中的
其他耗能，如热量。由此引入损伤耗能修正系数 λ ，并根据实测的试验曲线确定 λ值，进而定义损伤
变量，建立损伤演化方程。研究表明，采用该方法得到的混凝土损伤演化过程与试验曲线更吻合。

２ ＣＤＰ模型和 Ｎａｊａｒ能量损伤理论

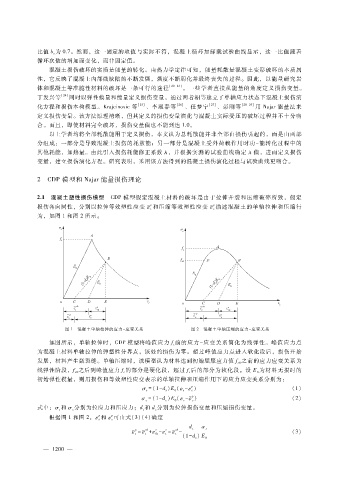
２．１ 混凝土塑性损伤模型 ＣＤＰ模型假定混凝土材料的破坏是由于拉伸开裂和压缩破碎所致，假定
ｐ ｐ
ε和压缩等效塑性应变 珔 ｃ
损伤各向同性，分别以拉伸等效塑性应变 珔 ｔ ε描述混凝土的单轴拉伸和压缩行
为，如图 １和图 ２所示。

图 １ 混凝土单轴拉伸的应力－ 应变关系 图 ２ 混凝土单轴压缩的应力－ 应变关系

如图所示，单轴拉伸时，ＣＤＰ模型将峰值应力 ｆ前的应力 － 应变关系简化为线弹性。峰值应力点
ｔ
为混凝土材料单轴拉伸的弹塑性分界点，该处的损伤为零。超过峰值应力点进入软化段后，损伤开始
发展，材料产生微裂缝。单轴压缩时，该模型认为材料达到初始屈服应力值 ｆ之前的应力应变关系为
ｃ０
线弹性阶段，ｆ之后到峰值应力 ｆ的部分是硬化段，超过 ｆ后的部分为软化段。设 Ｅ为材料无损时的
ｃ
ｃ０
０
ｃ
初始弹性模量，则用损伤和等效塑性应变表示的单轴拉伸和压缩作用下的应力应变关系分别为：
ｐ
－ ε） （１）
σ ｔ ＝ （１ － ｄ）Ｅ（ ε ｔ 珔 ｔ
ｔ
０
ｐ
－ ε） （２）
０
ｃ
σ ｃ ＝ （１ － ｄ）Ｅ（ ε ｃ 珔 ｃ
分别为拉应力和压应力；ｄ和 ｄ分别为拉伸损伤变量和压缩损伤变量。
ｔ ｃ
式中：σ ｔ 和 σ ｃ
ｐ ｐ
根据图 １和图 ２， 珔 ｔ ε可由式（３）（４）确定
ε和 珔 ｃ
ｄ ｔ σ ｔ
ｐ
ｅ
ｃｋ
ｃｋ
ｅ
ε＝ ε ＋ － ＝ ε － （３）
珔 ｔ 珔 ｔ ε ０ｔ ε ｔ 珔 ｔ
（１ － ｄ）Ｅ
ｔ ０
— １ ２ ０ —
０