Page 61 - 2024年第55卷第11期

考虑到本文模拟的察隅地震为 Ｍｗ８．６级，衰减关系中的震级项为定值，故可视其为常数；因本文
场地模型均为基岩场地类型，未考虑地震动土层响应，因此这里不考虑场地效应，距离采用断层距，
考虑几何扩散及非弹性衰减项 ［２９］ 。综上，选用考虑近断层饱和效应的强震动衰减模型如下：
ｌｇＹ ＝ ｃ＋ ｃ·ｌｇ（Ｒ ＋ Ｒ） ＋ ε （１０）
０
２
１
式中：Ｙ为地震动参数，这里主要考虑 ＰＧＡ、ＰＧＶ和 ＰＧＤ；ｃ和 ｃ为拟合系数；Ｒ为断层距，单位为
１ ２
ｋｍ；Ｒ为近场饱和因子，针对 Ｍｗ８．６级大震取 Ｒ ＝ ３０ｋｍ ［３０］ 。
０
０
采用非线性最小二乘回归分析方法对地震动峰值随断层距变化的规律拟合分析，得到对应的衰减
关系式系数见表 ４，图 ８为测点参数值散点图和拟合曲线图。
表 ４ 单、双断层模型地震动衰减关系式拟合系数
模型 参数 分量 ｃ １ ｃ ２ 可决系数 模型 参数 分量 ｃ １ ｃ ２ 可决系数
ＥＷ ２．００２ － ０．８５７ ０．６１２ ＥＷ ３．５８０ － ０．８２５ ０．５４９
ＰＧＡ ＮＳ １．７３４ － ０．６９２ ０．４９８ ＰＧＡ ＮＳ ３．７４１ － ０．８６１ ０．５０９
ＵＤ １．７８２ － ０．８１３ ０．７３４ ＵＤ ３．５９１ － ０．７１０ ０．４６９
ＥＷ １．９８３ － １．０３０ ０．６５５ ＥＷ ２．９４０ － ０．７８９ ０．５６７
单断层 双断层
ＰＧＶ ＮＳ １．７１５ － ０．８７６ ０．５４７ ＰＧＶ ＮＳ ３．１５８ － ０．８４８ ０．５５１
模型 模型
ＵＤ １．８７２ － １．０５６ ０．７９３ ＵＤ ３．０６２ － ０．７２３ ０．４８７
ＥＷ ２．０６３ － ０．８２４ ０．３８７ ＥＷ ２．８２８ － ０．６１４ ０．２７８
ＰＧＤ ＮＳ １．９７９ － ０．７５４ ０．３３２ ＰＧＤ ＮＳ ３．７２５ － ０．８９８ ０．４８４
ＵＤ ２．２２６ － １．０８９ ０．５２９ ＵＤ ３．５４９ － ０．９２０ ０．３５７

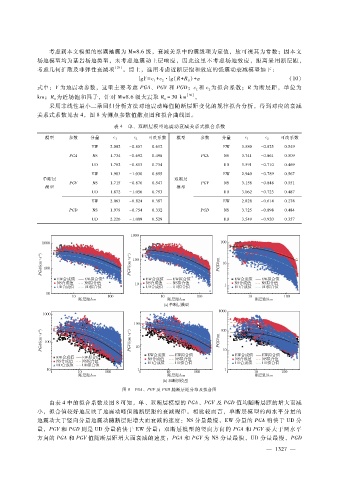
图 ８ ＰＧＡ、ＰＧＶ及 ＰＧＤ随断层距分布及拟合图

由表 ４中的拟合系数及图 ８可知，单、双断层模型的 ＰＧＡ、ＰＧＶ及 ＰＧＤ值均随断层距的增大而减
小，拟合值较好地反映了地震动峰值随断层距的衰减规律。相比较而言，单断层模型的两水平分量的
地震动大于竖向分量地震动随断层距增大而衰减的速度：ＮＳ分量最慢，ＥＷ 分量的 ＰＧＡ稍快于 ＵＤ分
量，ＰＧＶ和 ＰＧＤ则是 ＵＤ分量稍快于 ＥＷ 分量；双断层模型的竖向方向的 ＰＧＡ和 ＰＧＶ要大于两水平
方向的 ＰＧＡ和 ＰＧＶ值随断层距增大而衰减的速度：ＰＧＡ和 ＰＧＶ为 ＮＳ分量最快，ＵＤ分量最慢，ＰＧＤ
３
— １ ２ ７ —