Page 64 - 2024年第55卷第12期

４ 模型求解方法

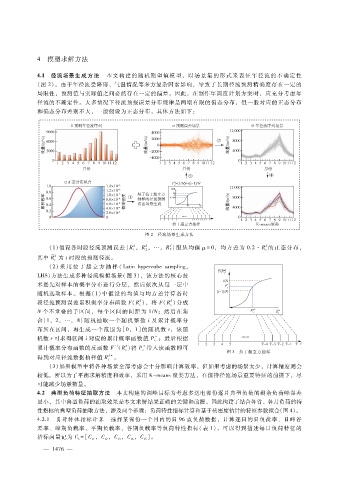
４．１ 径流场景生成方法 本文构建的随机期望值模型，以 场 景集 的形 式来 表征 年径 流的 不 确定性
（图 ２）。由于年径流受降雨、气温情况等多方复杂因素影响，导致了长期径流预测精确度存在一定的
局限性，预测值与实际值之间必然存在一定的偏差。因此，在制作年调度计划方案时，应充分考虑年
径流的不确定性。大多情况下径流预报误差分布规律是两端有限的偏态分布，但一般对应的正态分布
和偏态分布差别不大，一般假设为正态分布，具体方法如下：

图 ２ 径流场景生成方法

ｄ
ｄ
ｄ
ｄ
（１）假设各时段径流预测误差｛Ｒ，Ｒ，…，Ｒ ｝服从均值 μ ＝ ０，均方差为 ０．２· 珔 的正态分布，
Ｒ
ｔ
１
２
Ｔ
ｄ
其中 珔 为 ｔ时段的预测径流。
Ｒ
ｔ
（２）采 用 拉 丁 超 立 方 抽 样 （Ｌａｔｉｎｈｙｐｅｒｃｕｂｅｓａｍｐｌｉｎｇ，
ＬＨＳ）方法生成多种径流模拟场景（图 ３），该方法的核心技
术是先对样本的概率分布进行分层，然后依次从每一层中
随机选取样本。根据（ １）中假设的均值与均方差计算各时
ｄ
ｄ
段径流预测误差累积概率分布函数 Ｆ（Ｒ），将 Ｆ（Ｒ）分成
ｔ ｔ
Ｎ个不重叠的子区间，每个区间的间距为 １?Ｎ；然后在集
合｛１，２，…，Ｎ｝随机抽取一个随机整数 ｉ及累计概率分
布所在区间，再生成一个范围为［ ０，１］的随机数 ｒ，该随

机数 ｒ可求得区间 ｉ对应的累计概率函数值 Ｐ ；最后根据
ｔ
－ １
ｄ

累计概率分布函数的反函数 Ｆ （Ｒ）将 Ｐ 带入该函数即可
ｔ
ｔ
图 ３ 拉丁超立方抽样
ｄ 
得到对应径流数据抽样值 Ｒ 。
ｔ
（ ３）如果模型中将各种场景全部考虑会十分影响计算效率，但如果考虑的场景太少，计算精度则会
较低。所以为了平衡求解精度和效率，采用 Ｋ － ｍｅａｎｓ聚类方法，在保持径流场景重要特征的前提下，尽
可能减少场景数量。
４．２ 典型负荷特征抽取方法 本文构建的调峰目标为考虑多送电省份逐月典型负荷的剩余负荷峰谷差
最小，其中典型负荷的抽取效果是本文求解结果正确的关键和前提。因此构建了结合各省、各月负荷的特
性指标的典型负荷抽取方法，涉及两个步骤：负荷特性指标计算和基于核密度估计的特征参数拟合（图 ４）。
４．２．１ 负荷特性指标计算 选择某省份一个月内的日 ９６点负荷数据，计算逐日的日负荷率、日峰谷
差率、峰期负载率、平期负载率、谷期负载率等负荷特性指标（表 １），可以得到描述每日负荷特征的
指标向量记为 Ｃ＝ ［Ｃ ，Ｃ ，Ｃ ，Ｃ ，Ｃ ］。
ｔ２
ｔ１
ｔ
ｔ５
ｔ４
ｔ３
— １ ４ ６ —
７