Page 66 - 2024年第55卷第12期

（１）采用核密度估计对每项负荷特性指标进行密度函数拟合，根据各项负荷特性指标概率密度最
大的点，得到典型日负荷特性指标向量 ＣＴＰ＝ ［ＣＴＰ ，ＣＴＰ ，ＣＴＰ ，ＣＴＰ ，ＣＴＰ ］。
ｔ ｔ１ ｔ２ ｔ３ ｔ４ ｔ５
（ ２）根据欧式距离 ｄ评估各日负荷特性指标向量与典型负荷特性指标向量的距离，使用欧式距离
ｔ
倒数的幂指数衡量曲线权重，具体公式如下：
５
ｄ＝ ∑ （ｍ － ＣＴＰ） ２
ｊ
ｔｊ
ｔ 槡
ｊ ＝１
（２２）
（１?ｄ）
ｗ＝ Ｔ ｔ
ｔ
∑ （１?ｄ）
ｔ
ｔ ＝１
（３）使用各日负荷曲线根据上步所得权重叠加计算，得到最终需要的典型日负荷曲线。Ｌ＝ ［ｌ ，
ｔ ｔ，１
ｌ ，…，ｌ ］为 ｔ日的 ９６点负荷曲线，典型负荷曲线 ＬＴＰ （ｈ ＝ １ ，２，…，９６）计算公式如下：
ｔ，２ ｔ，９６ ｔ，ｈ
Ｔ
ｈ ∑
ＬＴＰ ＝ （ｗ·ｌ ） （２３）
ｔ，ｈ
ｔ
ｔ ＝１
４．３ 不同市场背景下模型求解策略
４．３．１ 全计划电量模式曲线分解 全计划电量模式下，巨型流域梯级需要确定各电站逐月的计划电量
总量以及送不同省份的典型出力曲线，有效响应各电网复杂调峰需求，这一任务与电站来水及受端电
网的短期负荷 特 性 密 切 相 关。 因 此， 曲 线 分 解 采 用 多 受 端 电 网 综 合 调 峰 目 标 （式 （ １））。 约 束 为
式（４）—（１５），包含水电常规约束、分时曲线相关约束。
４．３．２ 计划电量与市场化电量共存的曲线分解 在计划电量与市场化电量并存模式下，巨型流域梯级
电站在年前需要确定各省逐月计划和市场化电量，以及与计划电量的各省逐月典型出力曲线，其中计
划电量在各月间分配比例以及分时曲线形状均会影响市场化电量的决策空间，这种情况下月度电量需
求、日内负荷变化、径流特性都会影响计划电量和市场化电量的优化配置。因此，曲线分解采用式（２）
收益最大目 标，约 束 在 全 计 划 电 量 曲 线 分 解 基 础 上，进 一 步 考 虑 了 计 划 电 量 履 约 约 束 （式 （１６）—
（１８）），并将各电网调峰需求描述为适合的调峰边界，见式（１９）。
本文将不同阶段下的曲线分解任务均构建为混合整数规划（ ＭＩＬＰ）问题，涉及多时间维度、多受
端省份、梯级多个电站对象，求解难度复杂。通过对上述模型的求解，确定了年度逐月水位控制准
则、计划电量在各电站、各月、各省分配的结果、市场化电量在各电站、各月、各省分配的结果。

５ 实例分析

以西南某特大流域水电基地为依托工程，研究分析现阶段全计划电量模式下曲线分解，并前瞻性
探索未来计划电量与市场化电量并存阶段多受端电网的年度曲线分解及市场化电量决策问题。该流域
梯级是 “西电东送” 骨干电源，涉及广东、广西、云南、江苏、四川、浙江、上海 ７个送电省市，选取
某年梯级电站径流资料生成径流场景，以全年逐日 ２４点负荷数据为基础提取 ７个受端区域的典型负荷。
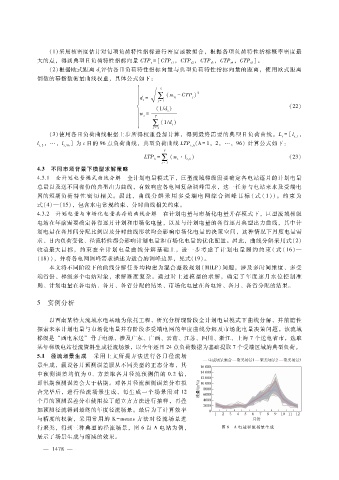
５．１ 径流场景生成 采用上文所提方法进行各月径流场
景生成，假设各月预测误差服从不同类型的正态分布，其
中预测误差均值为 ０、方差取各月径流预测值的 ０．２倍，
即汛期预测误差会大于枯期。对各月径流预测误差分布拟
合完毕后，进行径流场景生成，每生成一个场景需对 １２
个月的预测误差分布使用拉丁超立方方法进行抽样，再叠
加预测径流得到最终的年度径流场景。最后为了计算效率
与精度的权衡，采用常用的 Ｋ － ｍｅａｎｓ方法对径流场景进
行聚类，得到三种典型的径流场景，图 ６以 Ａ电站为例， 图 ６ Ａ电站径流场景生成
展示了场景生成与缩减的效果。

— １ ４ ８ —
７