Page 65 - 2024年第55卷第12期

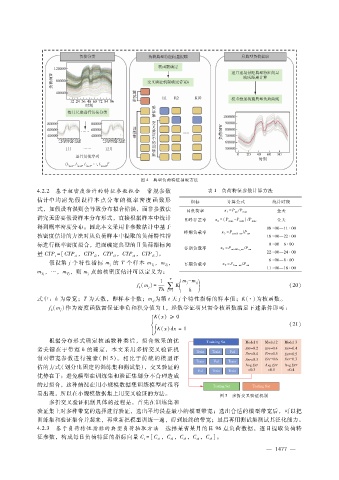
图 ４ 典型负荷特征抽取方法
４．２．２ 基于核密度估计的特征参数拟合 常规参数 表 １ 负荷特征参数计算方法
估计中均 需 先 假 设 样 本 点 分 布 的 概 率 密 度 函 数 形 指标 计算公式 统计时段
式，如假设有误则会导致分布拟合错误，而非参数法 ＝
日负荷率 ｘ １ Ｐ ａｖ ?Ｐ ｍａｘ 全天
讲究无需要假设样本分布形式，直接根据样本中统计 日峰谷差率 ｘ ２ （Ｐ ｍａｘ Ｐ ｍｉｎ ）?Ｐ ｍａｘ 全天
＝
－
得到概率密度分布。因此本文采用非参数估计中基于 ０８∶００—１１∶００
＝
峰期负载率 ｘ ３ Ｐ ｐｅａｋ＿ａｖ ?Ｐ ａｖ
核密度估计的方法对从负荷样本中提取的负荷特性指 １８∶００ —２２∶００
标进行概率密度拟合，进而确定典型的日负荷指标向 ０∶００—６∶００
＝
谷期负载率 ｘ ４ Ｐ ｍｉｄｄｌｅ＿ａｖ ?Ｐ ａｖ
量 ＣＴＰ＝ ［ＣＴＰ ，ＣＴＰ ，ＣＴＰ ，ＣＴＰ ，ＣＴＰ ］。 ２２∶００—２４∶００
ｔ２
ｔ１
ｔ
ｔ５
ｔ４
ｔ３
６∶００—８∶００
假设第 ｊ个特性指标 ｍ 的 Ｔ个 样本 ｍ ，ｍ ， 平期负载率 ｘ ５ Ｐ ｌｏｗ＿ａｖ ?Ｐ ａｖ
＝
ｊ
２ｊ
１ｊ
１１∶００—１８∶００
ｍ ，…，ｍ ，则 ｍ 点的核密度估计可以定义为：
３ｊ Ｔｊ ｊ
１ Ｔ ｍ－ ｍ ｔｊ
ｊ
ｆ（ｍ） ＝ ∑ Ｋ ( ) （２０）
ｋ ｊ
Ｔｈ ｔ ＝１ ｈ
式中：ｈ为带宽；Ｔ为天数，即样本个数；ｍ 为第 ｔ天 ｊ个特性指标的样本值；Ｋ（·）为核函数。
ｔｊ
ｆ（ｍ）作为密度函数需保证非负和积分值为 １，经数学证明只需令核函数满足下述条件即可：
ｊ
ｋ
{ Ｋ（ｘ）≥ ０ （２１）
∫
Ｋ（ｘ）ｄｘ ＝１
根据分布形式确定核函数种类后，拟合效果的优
劣关键在于带宽 ｈ的确定，本文采用多折交叉验证机
制对带宽参数进行搜索（图 ５）。相比于传统的模型评
估的方式（划分出固定的训练集和测试集），交叉验证的
优势在于：避免模型在训练集和验证集划分不合理造成
的过拟合，这种情况在用小规模数据集训练模型时很容
易出现，所以在小规模数据集上用交叉验证的方法。
图 ５ 多折交叉验证机制
多折交叉验证机制具体的过程是，首先在训练集和
验证集上对多种带宽的选择进行验证，选出平均误差最小的模型带宽；选出合适的模型带宽后，可以把
训练集和验证集合并起来，再重新把模型训练一遍，得到最终的带宽；最后再用测试集测试其泛化能力。
４．２．３ 基于负荷特性指标的典型负荷抽取方法 选择某省某月的日 ９６点负荷数据，逐日提取负荷特
征参数，构成每日负荷特征的指标向量 Ｃ＝ ［Ｃ ，Ｃ ，Ｃ ，Ｃ ，Ｃ ］。
ｔ２
ｔ１
ｔ
ｔ４
ｔ５
ｔ３
４
— １ ７ ７ —