Page 23 - 2025年第56卷第7期

积分后显式表达如下（参见图 7）
ì ê ê( ) 1 - m ù ú ú
é
ï ï A 0 t 0 ê ê t + t 0 - 1
ï
ú ú
ï 1 - m ∙ - 1 ， m ≠ 1
ï ï
ï ï ( ) m = 1
ε creep = í ë t 0 û （16）
ï ï
ï
t + t 0
ïA 0 t 0 ∙ ln
î
t 0

图 6 蠕变应变累积过程（蠕变速率分段描述） 图 7 蠕变应变累积过程（蠕变速率连续描述）

4 蠕变过程数学模型的初步验证

采用图 4 中案例对应的多个相同蠕变应力、不同加载历史下的蠕变实验成果，验证了提出的蠕变
发展过程数学描述的适用性。
对于图 4 中 600、80、2.24 和 1.67 kPa/min 等 4 种先期应力速率，以最高先期应力速率（600 kPa/min）
的方案为基准，计算蠕变中后期应变速率与时间关系在双对数坐标中的斜率 m （本例 m = 1.11），并将
该部分蠕变应变速率的对数-时间的对数关系直线向纵轴延伸形成蠕变基线，在纵坐标上的截距即初
始蠕变应变速率（10 min ）也视为阶跃加载时的基准蠕变速率初始值 A。
-3
-1
考虑蠕变前先期加载过程引起的不同初始蠕变速率 A 0 时，忽略不同应力速率加载时可能存在的速率
效应，即认为在相同的蠕变应力下压缩模量 E s 相同，根据 ε ̇ = σ ̇ /E s ，可按照基准蠕变速率初始值 A （对应先
期应力速率为 600 kPa/min）相应计算其他加载速率下的初始蠕变速率 A 0 ，并计算各方案蠕变弛豫时间 t 0 。
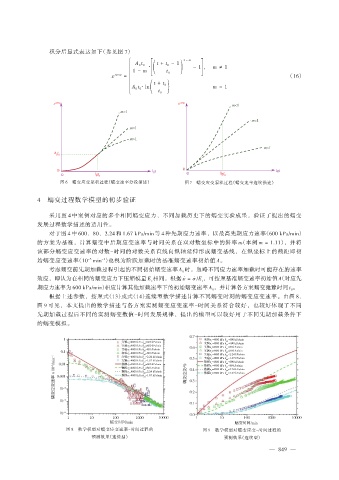
根据上述参数，按照式（13）或式（14）连续型数学描述计算不同蠕变时刻的蠕变应变速率。由图 8、
图 9 可见，本文提出的数学描述与各方案实测蠕变应变速率-时间关系符合较好，也较好体现了不同
先期加载过程后不同的实测蠕变数值-时间发展规律，提出的模型可以较好用于不同先期加载条件下
的蠕变模拟。

图 8 数学模型对蠕变应变速率-时间过程的 图 9 数学模型对蠕变应变-时间过程的
预测效果（连续型） 预测效果（连续型）

— 849 —