Page 66 - 2025年第56卷第7期

表 2 算例设计详情
算法迭
算例 配置 规格 算法 洪水场次 并行核数
代次数
Case1 MOGEO/NSGA-Ⅲ 1 1 1000
12th Gen Intel（R）Core（TM）i7-12700

Case2 单物理机（环境 1） MOGEO 1000/360 1 1000
@2.1GHz，12CPU，16GB RAM
Case3 MOGEO 360 2/4/6/8/12 1000
Case4 云服务器（环境 2） ecs.hfc7.8xlarge，32vCPU，64GiB RAM MOGEO 360 2/4/6/8/12/16 1000
6
3
Case5 分布式集群（环境 3） 6（ecs.hfc7.8xlarge，2vCPU，4GiB RAM） MOGEO 360 24/36/48/60/72 1000
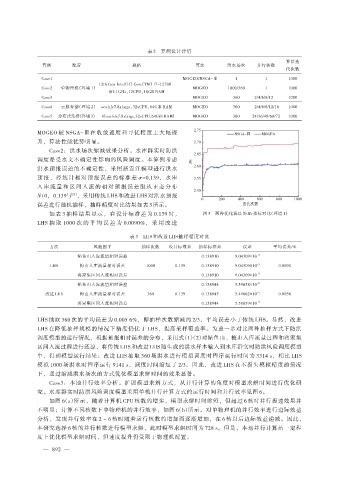
MOGEO 较 NSGA-Ⅲ在收敛速度和寻优精度上大幅提
升，算法性能优势明显。
Case2：洪水场次缩减效果分析。水库群实时防洪
调度是受水文不确定性影响的风险调度。本算例考虑
洪水预报误差的不确定性，采用新安江模型进行洪水
预报，经统计相对预报误差的标准差 σ=0.139，水库
入 库 流 量 和 区 间 入 流 的 相 对 预 报误差服从正态分布
2 ［23］
N (0，0.139 ) ，采用传统 LHS 和改进 LHS 对洪水预报
误差进行随机抽样，抽样精度对比结果如表 3 所示。
如表 3 抽样结果显示，在设计标准差为 0.139 时， 图 5 两种优化算法的 Hv 指标对比（环境 1）
LHS 抽 取 1000 次 的 平 均 误 差 为 0.0090%， 采 用 改 进

表 3 LHS 和改进 LHS 抽样精度对比

方法 风险因子 抽样次数 设计标准差 抽样标准差 误差 平均误差/%
鲇鱼山入库流量相对误差 0.138910 9.04309×10 -5
LHS 梅山入库流量相对误差 1000 0.139 0.138910 9.04309×10 -5 0.0090
蒋家集区间入流相对误差 0.138910 9.04309×10 -5
鲇鱼山入库流量相对误差 0.138944 5.59658×10 -5
改进 LHS 梅山入库流量相对误差 360 0.139 0.138945 5.49662×10 -5 0.0056
蒋家集区间入流相对误差 0.138944 5.58659×10 -5

LHS 抽取 360 次的平均误差为 0.005 6%，即抽样次数缩减约 2/3，平均误差小于传统 LHS。显然，改进
LHS 在降低抽样规模的情况下精度仍优于 LHS，提高采样覆盖率。为进一步对比两种抽样方式下防洪
调度模型的运行情况，根据预报相对误差的分布，采用式（1）（2）对鲇鱼山、梅山入库流量过程和蒋家集
区间入流过程进行还原，将传统 LHS 和改进 LHS 随生成的洪水样本输入到水库群实时防洪风险调度模型

中，得到模型运行结果：改进 LHS 抽取 360 场洪水进行模拟调度时程序运行时间为 3314 s，相比 LHS
模拟 1000 场洪水时程序运行 9141 s，调度时间缩短了 2/3。因此，改进 LHS 在不损失模拟精度的情况
下，通过缩减洪水场次的方式优化模型求解时间的效果显著。
Case3：本地并行效率分析。扩展模型求解方式，从并行计算的角度对模型求解时间进行优化研
究。水库群实时防洪风险调度模型采用单机并行计算方式的运行时间和并行效率见图 6。
如图 6（a）所示，随着计算机 CPU 核数的增多，模型求解时间缩短，但超过 6 核时并行提速效果并
不明显；计算不同核数下单物理机的并行效率，如图 6（b）所示。对单物理机的并行效率进行边际效益
分析，发现并行效率在 2 ~ 6 核时随着运行核数的增加而逐渐增加，在 6 核以后边际效益递减。因此，
本研究选择 6 核的并行核数进行模型求解，此时模型求解时间为 728 s。但是，本地并行计算虽一定程
度上优化模型求解时间，但速度提升仍受限于物理机配置。

— 892 —