Page 99 - 2025年第56卷第7期

体积模量，G (D )、K (D )可用 G 0 、K 0 表示为：
*
*
ï ï * * ]
ìG (D ) = (1 - η rf D)G 0 = E (D )/[ 2(1 + v)
í ] （22）
î * *
ï ïK (D ) = (1 - η rf D) K 0 = E (D )/[ 3(1 - 2v)
由式（22）可知，损伤最终表现为弹性模量的
退化。相应地，如图 4 所示，经损伤修正后的应
力-应变曲线呈现出应变软化现象，反映了材料力

学性能的劣化。
随着材料内部损伤的积累，其抵抗进一步塑
性变形的能力会下降，弹塑性损伤模型的屈服准
则受硬化参数和损伤变量影响（硬化过程屈服面扩
［38-39］
张，软化过程屈服面收缩） 。根据应变等价原
理，有效应力状态下计算得到的应力不变量 I 1 、J 2
͂
值可分别表示为 I 1 = I 1 / (1 - D)，J 2 = J 2 / (1 - D) 。
͂
2
则考虑损伤效应的剪切屈服函数以应力不变量的
形式表示为： 图 4 弹塑性损伤模型刚度退化及应力损伤修正
2 J 2 cosθ 4 J 2 cosθ
*
q a
F s = - - (1 - D )γ p （23）
*
E 50 q a - 2 E ur
J 2 cosθ/ (1 - D )
同理，考虑损伤效应的“帽盖”屈服函数表示为：
( ( 3 ( δ - 1) sin θ ) ) 2
J 2 ( δ + 1) cos θ +
*
F v = + I 1 2 - (1 - D )P c 2 （24）
(1 - D )M 2 9(1 - D )
*
*
1
式中 θ 为应力洛德角，θ = arccos ((J 3 /2)/ ((J 2 /3) 3/2 ))。
3
3 本构模型数值实现及试验验证
数值积分算法是本构模型数值实现的核心环节。本节基于前向 Euler 积分算法与 Runge-Kutta 迭代
方案编写 UMAT 子程序，经编译调试后对塑性混凝土的三轴试验进行有限元模拟，并与室内试验结果
进行比较，以验证子程序的有效性。
3.1 UMAT 子程序编制

（1）本构积分算法。根据胡克定律的假设，基于 t n
时刻的应力 { σ n }和应变增量 { Δε n + 1 }，通过弹性刚度
矩阵 [ C ]更新 n+1 步的应力增量 { σ n + 1 }，即：
e
trial
trial e
{ σ n + 1 } = { σ n } + [ C ] { Δε n + 1 } （25）
由于增量形式的广义胡克定律应用的是切线弹性
模量 E，而 HS 模型切线模量应用的是加载模量 E 50 ，
为 便 于 求 解 式（25）中 的 弹 性 刚 度 矩 阵 [ C ]， 需 要 在
e
ε 1 - q 坐标平面内 ［40］ 建立切线弹性模量 E 和加载模量
E 50 之间的关系式：
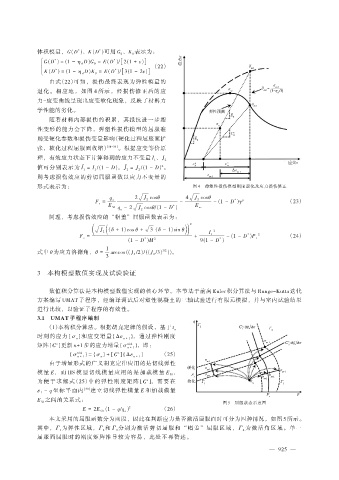
图 5 屈服状态示意图
2
E = 2E 50 (1 - q/q a ) （26）
本文采用的屈服函数分为两段，因此在判断应力是否激活屈服面时可分为四种情况，如图 5 所示。
其中，Γ 为弹性区域，Γ 和 Γ 分别为激活剪切屈服和“帽盖”屈服区域，Γ 为激活角区域。单一
1 2 3 4
屈服面屈服时的刚度矩阵推导较为容易，此处不再赘述。

— 925 —