Page 97 - 2025年第56卷第7期

（9）
σ 1 = Eε 1( 1 - η rf D) + 2vσ 3
( ( ) k ) ( ( λ ( ) k - 1 ) )
对式（9）在峰值应力处的微分结果化简可得：
)
exp - ε sc - ε 1d = ( η rf - 1 / η rf 1 - kε sc ε sc - ε 1d （10）
λ
λ
( ( ) k ) 1
在峰值应力处，应力-应变关系满足下式：

exp - ε sc - ε 1d = σ sc - 2vσ 3 + 1 - η rf （11）
λ
η rf Eε sc
( η rf - 1 ) ) ) ( ( σ sc - 2vσ 3 1 ) )
式（11）由式（9）在峰值应力处转化得到。联立式（10）（11）可得 k 和 λ 解析式：

( η rf - 1 ) ) -1 ) 1/k
k = - ( ε sc - ε 1d ) 1 - / ε sc ln η rf Eε sc + 1 - η rf （12）
( ( (σ sc - 2vσ 3 )/ (Eε sc ) + η rf - 1
1 -
λ = ( kε sc( ε sc - ε 1d ) k - 1 )( ( (σ sc - 2vσ 3 )/ (Eε sc ) + η rf - 1 （13）

通过上式可知，参数 k 和 λ 是关于 σ 、ε 、η 的函数关系式，其中 η 是关于 σ 的函数，见式（6）。
sc sc rf rf rf
由于塑性混凝土的峰值强度和残余剪切强度随围压的变化而呈现非线性变化，为便于上述损伤模型的
应用，同时也为了能适用于任意围压下变形过程的模拟，需建立 σ 、ε 、σ 的确定方法 ［26］ 。本文基
sc sc rf
于已有的研究，建立如下损伤参数确定方法：
ìσ sc = (2c cos φ + σ 3 (1 + sin φ) )/ (1 - sin φ)
ï ï ï ï
í ε sc = aσ 3 + b （14）
ï ï
î β rf
ï ï σ rf = α rf σ 3
式中：a、b 为常数，通过不同围压下应力峰值点对应的应变拟合确定；α 、β 通过不同围压下残余应
rf rf
力拟合确定。
基于上述建立的损伤参数确定方法，研究损
伤参数对损伤演化规律的影响。将塑性混凝土损
伤参数代入损伤模型中进行分析，由图 2 可知，
常规统计损伤方程引入损伤阈值后，损失阈值
（局部放大图可见） 可将损伤变量演化曲线分为
未损伤（弹性）阶段与发生损伤（塑性屈服）阶段，
该分阶段演化特征符合材料在弹性阶段刚度不
变、无损伤产生或损伤程度极小可以忽略的理
论 ［27］ 。除此之外，不同围压下的曲线损伤起始
点不同，是因为随着围压的增大，塑性混凝土抗
压能力增强，屈服点增高，同时损伤阈值也相
应增大；曲线末尾部分损伤变量随围压的增大
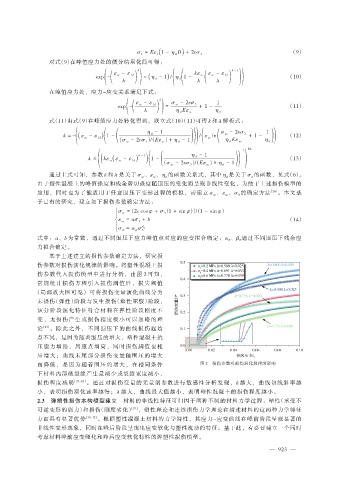
而降低，是因为随着围压的增大，在相同条件 图 2 损伤参数对损伤演化规律的影响
下材料内部微裂缝产生量减少或裂缝宽度减小，
损伤程度减弱 ［27-28］ 。通过对损伤变量的无量纲参数进行敏感性分析发现，k 越大，曲线切线斜率越
小，表明损伤演化速率越慢；λ 越大，曲线最大值越小，表明塑性混凝土的损伤程度越小。
2.3 弹塑性损伤本构模型建立 材料的非线性特征可归因于两种不同的材料力学过程：塑性（承受不
［29］
可逆变形的能力）和损伤（刚度劣化） ，塑性理论和连续损伤力学理论在描述材料的这两种力学特征
方面具有显著优势 ［30-32］ 。根据塑性混凝土材料的力学特性，其应力-应变曲线在峰前阶段呈现显著的
非线性变形现象，同时在峰后阶段呈现出应变软化与塑性流动的特征。基于此，有必要建立一个同时
考虑材料峰前应变硬化和峰后应变软化特性的弹塑性损伤模型。

— 923 —