Page 66 - 2025年第56卷第8期

a * - b * T - a * - b * T
2
2
2
2
e + e ( a * - b * )T a * - b * )T ) -1
2
2
2
2
上式中 K 1 = ，K 2 = e (-a ∗ + - e (-a ∗ - 。根据上文可知，冲刷稳定后半
a * - b * T - a * - b * T
2
2
2
2
e - e
椭球体局部冲刷坑体积 V T = πL P B P H P /6，则自冲刷特征控制体中输移 M PT 的泥沙在冲刷前孔隙率 δ 0 =
1 - πD M PT /( ) ，即求得塔基周围局部冲刷深度为：
3
6V T
M PT D 3
H P = （19）
(1 - δ 0 )L P B P
3.2 河床极限可动层厚度 所谓河床极限可动层厚度即自初始床面起算的塔基局部冲刷深度与一般
冲刷深度之和。在塔基周围发生局部冲刷时，由于塔基承台下桩间距相对较窄，则同一承台下桩群
往往起到联合冲刷的效果，故承台下桩群的最大间距 L 对塔基周围的河床可动层起到较大影响。同
B
时，试验观察可知水流强度和床沙粒径的影响也很重要。由此，引入水流相对强度指标 V /V ，即冲
C
m
刷前水流最大垂线流速 V 与床面泥沙临界起动流速 V 的比值。通过整理分析 9 种水流相对强度、7
C
m
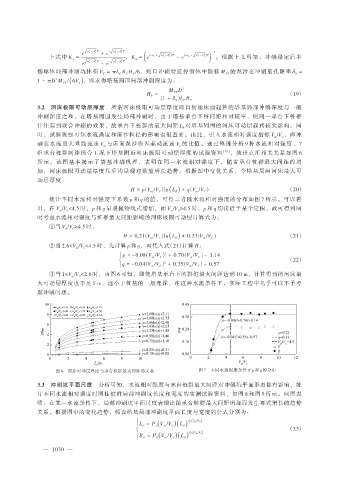
组承台桩群间距组合工况下塔基附近河床极限可动层厚度的试验资料 ［10］ ，统计点汇相关关系如图 6
所示。该图基本揭示了塔基冲刷机理，表明在同一水流相对强度下，随着承台桩群最大间距的增
加，河床极限可动层厚度几乎均呈现对数型增长趋势。根据图中变化关系，令塔基周围河床最大可
动层厚度：
H = p(V m /V C ) ln( L B) + q(V m /V C ) （20）
统计不同水流相对强度下系数 p 和 q 的值，可得二者随水流相对强度的分布如图 7 所示。可以看
出，在 V /V <4.5 时，p 和 q 呈现抛物线式增加，而 V /V ≥4.5 时，p 和 q 均接近于某个定值，故可得到同
C
C
m
m
时考虑水流相对强度与桩群最大间距影响的河床极限可动层计算式为：
①当 V /V ≥4.5 时，
C
m
H = 0.21(V m /V C ) ln( L B) + 0.33(V m /V C ) （21）
②当 2.6≤V /V <4.5 时，先计算 p 和 q，再代入式（21）计算 H：
m
C
2
ì p = -0.08(V m /V C ) + 0.70 (V m /V C ) - 1.14
í （22）
2
î q = -0.04(V m /V C ) + 0.35(V m /V C ) - 0.57
③当 1≤V /V <2.6 时，由图 6 可知，即使塔基承台下的群桩最大间距达到 10 m，计算得到的河床最
m
C
大可动层厚度也不足 1 m，远小于桩基的一般埋深，在这种水流条件下，实际工程中几乎可以不予考
虑冲刷问题。

图 6 河床可动层厚度与承台桩群最大间距的关系 图 7 不同水流强度条件下 p 和 q 的分布

3.3 冲刷坑平面尺度 分析可知，水流相对强度与承台桩群最大间距对冲刷坑平面形态都有影响，统
计不同水流相对强度时圆柱桩群局部冲刷坑长度和宽度的实测试验资料，如图 8 和图 9 所示。两图表
明：在某一水流条件下，局部冲刷坑平面尺度表现出随承台桩群最大间距增加而发生幂式增长的趋势
关系。根据图中的变化趋势，假设塔基局部冲刷坑平面长度与宽度的公式分别为：
ì L P = P L( V m /V C )( ) Q L( V m /V C )
ï ï
L B
í )( ) Q B( V m /V C ) （23）
î L B
ï ï ï ï B P = P B( V m /V C
— 1030 —