Page 47 - 水利学报2021年第52卷第2期

- -
Z 、 Z i，t 分别为电站 i 在时段 t 的库水位下限与上限，m； Qo 、 Q o 分别为电站 i 在时段 t 的出
- i，t - i，t i，t
-
--
-
库 流 量 下 限 与 上 限 ， m /s； Qe 、 Qe 分 别 为 电 站 i 在 时 段 t 的 发 电 流 量 的 下 限 与 上 限 ， m /s；
3
3
- i，t i，t
-
N 、 N i，t 分别为电站 i 在时段 t 的出力下限与上限，MW； Z 为调度期水电站 i 的初始库水位，
- i，t i，0
m； Z 为调度期末水电站 i 的库水位，m； V 为 t 时刻水电站 i 的水库水量，万 m ； Z 为 t 时刻
3
i，T i，t i，t
水电站 i 的水库水位，m； q i，t 为 t 时刻水电站 i 的下泄流量，m /s； h i，t 为 t 时刻水电站 i 的尾水位，
3
-
m； N 、 N it 分别为电站 i 在时段 t 的出力下限和上限，MW。
- it
3 耦合 KL 理论与调度特征的水电调度方法
3.1 总体思路 本文思路是采用谱优化方法中的 Karhunen-Loève 展开（以下简称 KL 展开），通过实际
调度历史样本分析与特征提取，将待优化调度决策看作一个需要进行模拟的随机过程，利用从样本
中提取的特征项构建随机过程表达式，通过特定分布的随机变量确定各个特征项的线性组合，有效
减少决策变量的个数，从而达到降维目的。KL 展开可以对复杂多变量随机过程进行高效处理，将其
描述为若干正交向量与特征值的展开式。其中，特征值和特征向量需要采用主成分分析方法，从水
电站群长系列实际调度样本进行识别提取；特征项的随机变量应该采用何种分布进行组合计算，需
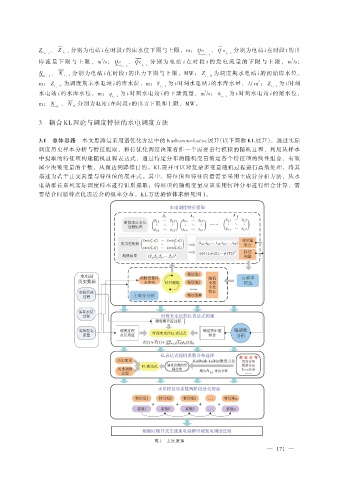
要结合问题特点优选适合的概率分布。KL 方法的整体求解见图 1。

A Ⅰ
A 1 A 2

ψ ψ ψ

M

D

n
n

图 1 方法原理
— 171 —