Page 80 - 水利学报2021年第52卷第4期

V LB = 0.654β 0 3.73 (1 + 1.653β sinθ ) （54）
∗
0
*
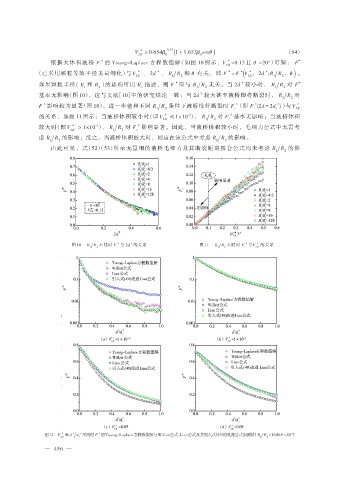
依据大体积液桥 F 的 Young-Laplace 方程数值解（如图 10 所示，V LB =0.13 且 θ =20°）可知： F *
∗
)
（已采用颗粒等效半径无量纲化）与 V LB 、 2d 、 R R 和 θ 有关，即 F = F ( V ，2d ，R R ，θ 。
∗
∗
∗
∗
∗
∗
LB
1
2
2
1
*
∗
如果颗粒半径（ R 和 R ）的影响可用 R 描述，则 F 应与 R R 无关。当 2d 较小时， R R 对 F *
1 2 e 1 2 1 2
基本无影响（图 10），这与文献［10］中的研究结论一致；当 2d 较大甚至液桥即将断裂时， R R 对
∗
1 2
*
F 影响较为显著（图 10）。进一步整理不同 R R 条件下液桥恰好断裂时 F （即 F (2d = 2d )）与 V ∗
∗
∗
∗
1 2 r r LB
的关系，如图 11 所示：当液桥体积较小时（即 V LB ≤1×10 ）， R R 对 F 基本无影响；当液桥体积
∗
∗
-3
r
2
1
较大时（即 V LB ＞1×10 ）， R R 对 F 影响显著。因此，当液桥体积较小时，毛细力公式中无需考
∗
∗
-3
r
1
2
虑 R R 的影响；反之，当液桥体积较大时，则应在该公式中考虑 R R 的影响。
1 2 1 2
由此可见，式（52）（53）所示无量纲的液桥毛细力及其断裂距离拟合公式均未考虑 R R 的影
1 2
*
*
*
图 10 R R 不同时 F 与 2d 的关系 图 11 R R 不同时 F 与 V LB * 的关系
r
1 2 1 2

*
∗
图12 V LB * 和 d ∗ d 不同时 F 的Young-Laplace方程数值解与Willett公式、ian公式及其引入式（49）的改进公式预测值（R R =16和θ =20°）
L
r
1
2
— 456 —