Page 79 - 水利学报2021年第52卷第4期

∗
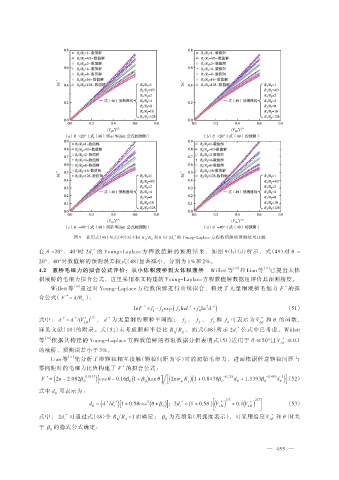
图 9 采用式（48）与式（49）对不同 R R 和 θ 时 2d 的 Young-Laplace 方程数值解的预测结果比较
r
1 2
∗
在 θ =20°、40°时 2d 的 Young-Laplace 方程数值解的预测结果，如图 9（b）（d）所示，式（49）对 θ =
r
20°、40°时数值解的预测误差较式（48）显著减小，分别为 1%和 2%。
4.2 液桥毛细力的拟合公式评价：从小体积液桥到大体积液桥 Willett 等 ［10］ 和 Lian 等 ［11］ 已提出大体
积液桥的毛细力拟合公式，这里采用本文构建的 Young-Laplace 方程数值解数据组评价其预测精度。
*
Willett 等 ［10］ 通过对 Young-Laplace 方程数值解进行曲线拟合，构建了无量纲液桥毛细力 F 的拟
*
合公式（ F = λ/R ）：
e
+
lnF = f - f exp( f lnd + f ln d + ) （51）
∗
2
1 2 3 4
*
*
*
+
式中： d = d /(V ) 1 2 ， d 为无量纲的颗粒半间距； f 、 f 、 f 和 f 可表示为 V LB 和 θ 的函数，
∗
LB
4
2
1
3
∗
详见文献［10］的附录。式（51）未考虑颗粒半径比 R R ，而式（48）所示 2d 公式中已考虑。Willett
1 2 r
∗
等 ［10］ 依据其构建的 Young-Laplace 方程数值解的有限数据分析表明式（51）适用于 θ ≤50°且 V LB ≤0.1
的液桥，预测误差小于 3%。
Lian 等 ［11］ 先分析了湿颗粒相互接触（颗粒间距为零）时的初始毛细力，进而依据任意颗粒间距与
*
零间距时的毛细力比值构建了 F 的拟合公式：
)
*
F = ( 2π - 2.082β 0.9197 )[ cos θ - 0.16β (1 + β tan θ ] [(2πσ R )( 1 + 0.8438β -0.724 d + 1.3393β -1.459 d 2 ] ) （52）
0 0 0 w e 0 θ 0 θ
式中 d 可表示为：
θ
é
) êV
d = ( d /d r ∗ )[ 1 + 0.5θcos (θ + β 0 ] ) ；2d = (1 + 0.5θ ( ) 1 3 + 0.1( V LB 2 3 ù ú ) û （53）
∗
∗
2
∗
∗
LB
θ
r
ë
式中： 2d 可通过式（48）令 R R =1 而确定； β 为充填角（用弧度表示），可采用给定 V LB 和 θ 时关
∗
∗
r
1
2
0
于 β 的隐式公式确定：
0
— 455 —