Page 74 - 水利学报2021年第52卷第4期

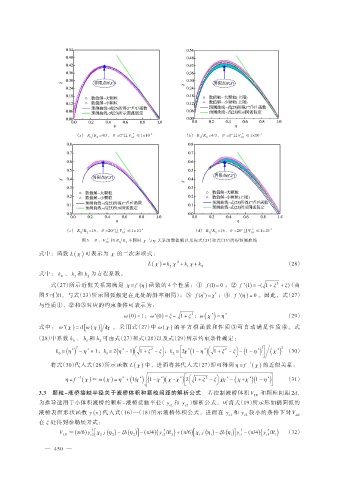
（a） R R =4/3、 θ =0°且 V * ≤1×10 -6 （b） R R =4/3、 θ =0°且 V * ≤1×10 -3
1 2 LB 1 2 LB

（c） R R =16、 θ =20°且 V * ≤1×10 -6 （d） R R =16、 θ =20°且 V * ≤1×10 -3
1 2 LB 1 2 LB
图 5 θ 、 V LB * 和 R R 不同时 χ 与 η 关系的数值解以及由式（25）和式（23）所得预测曲线
2
1
χ
式中：函数 L ( ) 可表示为 χ 的二次多项式：
χ
L ( ) = k χ + k χ + k （28）
2
2 1 0
式中： k 、 k 和 k 为方程系数。
0 1 2
η
式（27）所示近似关系需满足 χ = f ( ) 函数的 4 个性质：① f (1) = 0 ；② f ′( ) 1 = -( 1 + ξ + ξ)（由
2
*
*
η
图 5 可知，与式（23）所示圆弧假定在此处的斜率相同）；③ f (η ) = χ ；④ f ′( ) = 0 。因此，式（27）
与性质①、②和③对应的约束条件可表示为：
χ
ω ( ) 0 = 1；ω ′( ) 0 = ξ - 1 + ξ ；ω( ) = η ∗ （29）
∗
2
]
χ
χ
χ
式中： ω ′( ) = d [ω ( ) dχ 。采用式（27）中 ω ( ) 的平方根函数和性质③可自动满足性质④。式
（28）中系数 k 、 k 和 k 可由式（27）和式（28）以及式（29）所示约束条件确定：
0 1 2
)
2 ) æ 2 ö é ∗ æ ö 2 ù 2
η
χ
∗
∗
∗
∗
∗
2
k = ( ) - η + 1；k = 2(η - 1 1 + ξ - ξ ；k = ê2χ (1 - η 1 + ξ - ξ - (1 - η ∗ ú ) ( ) （30）
0 1 è ø 2 ë è ø û
χ
χ
将式（30）代入式（28）所示函数 L ( ) 中，进而将其代入式（27）即可得到 η = f ( ) 的近似关系：
-1
ö
∗ ∗
∗ ∗
χ
χ
η = f ( )≈ ω ( ) = η + (1/χ ∗ ) (1 - χ ∗ )( χ - χ ∗ é æ 1 + ξ - ξ χχ - ( χ + χ ∗ )(1 - η ∗ ù ú ) （31）
-1
2
) ê2
ë è ø û
3.3 颗粒-液桥接触半径关于液桥体积和颗粒间距的解析公式 若控制液桥体积 V LB 和颗粒间距 2d，
为推导适用于小体积液桥的颗粒-液桥接触半径（ y 和 y ）解析公式，可将式（19）所示形如椭圆弧的
c1 c2
液桥表面形状函数 y ( ) x 代入式（16）—（18）所示液桥体积公式，进而在 y 和 y 较小的条件下对 V
c1 c2 LB
在 ξ 处得到泰勒展开式：
]
]
)(
)(
)
η
η
V LB ≈(π/6 y c2[ χ j ( ) - ξh( ) - (π/4 y /R 2 ) + (π/6 )[ χ j ( ) - ξh( ) y - (π/4 y /R 1 ) （32）
η
η
4
3
3
4
2
c1
1
1
1
c2
c1
2
2
— 450 —