Page 70 - 水利学报2021年第52卷第4期

ì 4 { é 2 2
)(
)
ï ïδ = (R - R y + ξR y R - y 2 + R y ù 2 ξ + 1 - y R R ( ξ + } ) 1 + ξ R ( ξ + 1 y - y 2 )
2
2
2
2
2
2
2
2
ï ï ë 1 2 c2 1 c2 2 c2 2 0 û 0 1 2 2 0 c2
ï ï δ = 2 ê -ξR y y R - y 2 - R y y 2 ö ξ + 1 + R R y y ( ξ + ù ú ) 1 {[(R - R y +
é æ
)
2
2
2
2
2
2
2
ï ï 2 ë è 1 0 c2 2 c2 1 0 c2 ø 1 2 0 c2 û 1 2 c2
í （13）
)(
ï ï ξR y R - y 2 + R y ù 2 ξ + 1 - y R R ( ξ + } ) 1 - ξ R R ( ξ + 1 y - y 2 ) 2
2
2
2
2
2
2
2
2
ï ï 1 c2 2 c2 2 0 û 0 1 2 1 2 0 c2
ï ï é æ ù 2
ï ïδ = ê -ξR y y 2 R - y 2 - R y y 2 ö ξ + 1 + R R y y ( ξ + ú ) 1
2
2
2
2
2
î 0 ë è 1 c2 0 2 c2 1 c2 0 ø 1 2 0 c2 û
当两个颗粒半径相同时（ R = R ），式（12）有唯一解 y = y ，此时液桥也关于 y 轴对称。表征式
1 2 c1 c2
（12）所 示 方 程 存 在 实 解 的 判 别 公 式 为 Δ = δ - 4δ δ 。 该 方 程 存 在 两 个 实 解（ Δ＞0 ）、 一 个 实 解
2
2 4 0
（ Δ = 0）或无实解（ Δ＜0）均需满足条件 y ≤ y ≤ R 。当存在两个实解时，仅液桥表面积较小（其表
c2 c1 1
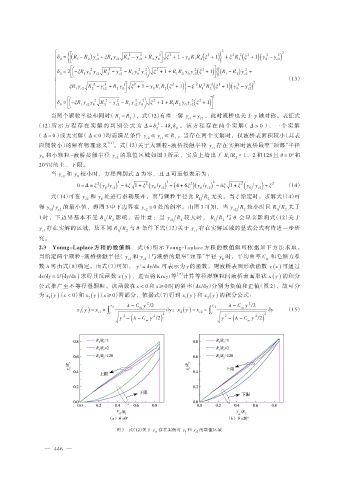
面能较小）的解有物理意义 ［12］ 。式（12）关于大颗粒-液桥接触半径 y 存在实解时液桥最窄“颈部”半径
c1
y 和小颗粒-液桥接触半径 y 的取值区域如图 3 所示，实质上给出了 R /R = 1、2 和 128 且 θ = 0°和
0 c2 1 2
20°时的上、下限。
当 y 和 y 较小时，方程判别式 Δ 为零，且 Δ 可近似表示为：
c2 0
2
2
3
0 = Δ » ξ ( y /y ) - 4ξ 1 + ξ ( y /y ) + ( 4 + 6ξ 2 )( y /y ) - 4ξ 1 + ξ ( y y ) + ξ 2 （14）
4
2
2
0 c2 0 c2 0 c2 0 c2
式（14）可在 y 和 y 处进行泰勒展开，而与颗粒半径比 R R 无关。当 ξ 给定时，求解式（14）可
c2 0 1 2
得 y y 的最小值，即图 3 中下边界在 y = 0 处的斜率。由图 3 可知，当 y R 较小时且 R R 大于
0 c2 c2 c2 2 1 2
1 时，下边界基本不受 R R 影响。需注意：当 y R 较大时， R R 与 θ 会显著影响式（12）关于
1 2 c2 2 1 2
y 存在实解的区域，故不同 R R 与 θ 条件下式（12）关于 y 存在实解区域的显式公式有待进一步研
c1 1 2 c1
究。
2.3 Young-Laplace 方程的数值解 式（6）所示 Young-Laplace 方程的数值解可依据如下方法求取。
当给定两个颗粒-液桥接触半径（ y 和 y ）与液桥的最窄“颈部”半径 y 时，平均曲率 C 和毛细力系
c1 c2 0 m
数 λ 可由式（8）确定。由式（7）可知， y ′ = dy/dx 可表示为 y 的函数，则液桥表面形状函数 y ( ) x 可通过
)
y
y
dx/dy = 1/(dy/dx 求得其反函数 x ( ) ，进而将 Kruyt 等 ［12］ 计算等径湿颗粒间液桥表面形状 x ( ) 的积分
公式推广至不等径湿颗粒。该函数在 x＜0 和 x≥0 时的斜率（dx/dy）分别为负值和正值（图 2），故可分
y
y
y
y
为 x ( )（x＜0）和 x ( )（x≥0）两部分，依据式（7）得到 x ( ) 和 x ( ) 的积分公式：
1 2 1 2
2
2
y λ - C y /2 y λ - C y /2
y
y
x ( ) = x + c1 m dy；x ( ) = x - c2 m dy （15）
1 c1  y 2 c2  y
2 2 ) 2 2 2 ) 2
y - ( λ - C y /2 y - ( λ - C y /2
m
m
图 3 式（12）关于 y 存在实解时 y 和 y 的取值区域
0
c2
c1
— 446 —