Page 72 - 水利学报2021年第52卷第4期

ì n = ( y x y ′ - y + y 2 ) [ x y ′ - 2( y - y ] )
2
ï i ci ci ci ci 0 ci ci ci 0
ï
ï
ï 2
(
í a = x 1 - é n - y ) (n - y ) ù （20）
ï i ci ë i ci i 0 û
ï
ï
ï b = n - y
î i i 0
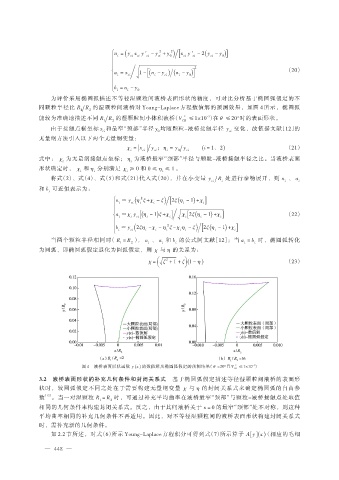
为评价采用椭圆弧描述不等径湿颗粒间液桥表面形状的精度，可对比分析基于椭圆弧假定的不
同颗粒半径比 R R 的湿颗粒间液桥对 Young-Laplace 方程数值解的预测效果，如图 4 所示，椭圆弧
1 2
能较为准确地描述不同 R R 的湿颗粒间小体积液桥（V ∗ ≤1×10 ）在 θ ≤20°时的表面形状。
-3
1 2 LB
由于接触点横坐标 x 和最窄“颈部”半径 y 均随颗粒-液桥接触半径 y 变化，故依据文献［12］的
ci
ci
0
无量纲方法引入以下两个无量纲变量：
χ = | x ci | y ；η = y 0 y ci (i = 1、2 ) （21）
i
i
ci
式中： χ 为无量纲接触点坐标； η 为液桥最窄“颈部”半径与颗粒-液桥接触半径之比。当液桥表面
i
i
形状确定时， χ 和 η 分别满足 χ ≥ 0 和 0 ≤ η ≤ 1 。
i
i
i
i
将式（2）、式（4）、式（5）和式（21）代入式（20），并在小变量 y ci R 处进行泰勒展开，则 n 、 a i
i
i
和 b 可近似表示为：
i
)
)
ì n ≈ y (η ξ + χ - ξ [ 2ξ(η - 1 + χ ]
2
ï i ci i i i i
ï
ï ) ] ) ]
ï
a ≈ χ y [(η - 1 ξ + χ
í i i ci i i χ [ 2ξ(η - 1 + χ i （22）
i
i
ï
ï
ï 2 ) ) ]
ïb ≈ y ( 2ξη - χ - η ξ - χ η - ξ [ 2ξ(η - 1 + χ
î i ci i i i i i i i
当两个颗粒半径相同时（ R = R ）， n 、 a 和 b 的公式同文献［12］；当 a = b 时，椭圆弧转化
1 2 i i i i i
为圆弧，即椭圆弧假定退化为圆弧假定，则 χ 与 η 的关系为：
ö
2
χ = æ ξ + 1 + ξ (1 - η ) （23）
è ø

-3
图 4 液桥表面形状函数 y ( ) x 的数值解及椭圆弧假定的预测结果（θ =20°且 V LB ∗ ≤1×10 ）
3.2 液桥表面形状的补充几何条件和封闭关系式 基于椭圆弧假定描述等径湿颗粒间液桥的表面形
状时，较圆弧假定不同之处在于需要构建无量纲变量 χ 与 η 的封闭关系式来确定椭圆弧的自由参
数 ［12］ 。当一对湿颗粒 R = R 时，可通过补充平均曲率在液桥最窄“颈部”与颗粒-液桥接触点处取值
1 2
相同的几何条件来构建封闭关系式。反之，由于其间液桥关于 x = 0 的最窄“颈部”处不对称，则这种
平均曲率相同的补充几何条件不再适用。因此，对不等径湿颗粒间的液桥表面形状构建封闭关系式
时，需补充新的几何条件。
如 2.2 节所述，对式（6）所示 Young-Laplace 方程积分可得到式（7）所示算子 Λ[ ] y ( ) x （相应的毛细

— 448 —