Page 77 - 水利学报2021年第52卷第4期

*
*
*
*
表 1 不同 θ 值对应的 χ 、 η 、 j 和 h 值
θ χ * η * j * h *
0° 0.4109 0.3599 1.6063 -0.6814
α
5° 0.4514 0.3567 1.5925 -0.6814
10° 0.4949 0.3546 1.5836 -0.6896

15° 0.5414 0.3541 1.5814 -0.6904
θ/( ) ° 20° 0.5910 0.3560 1.5895 -0.6874
图 6 文献［9］和式（46）中系数 α 与 θ 的关系

*
（a） R R =2 且 V LB * =1×10 或 1×10 -3 （b） R R =128 且 V LB =1×10 或 1×10 -3
-6
-6
1
1
2
2
*
*
*
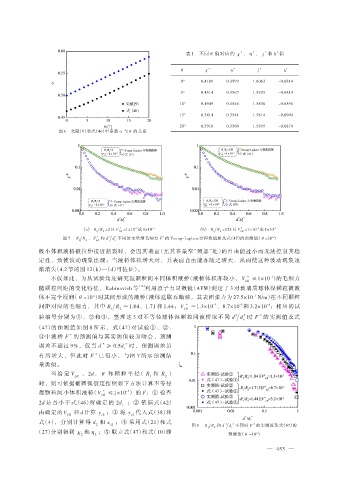
图 7 R R 、 V LB * 和 d d 不同时无量纲毛细力 F 的 Young-Laplace 方程数值解及式（47）的预测值（θ =20°）
r
2
1
极小体积液桥被拉伸接近断裂时，会因其表面（尤其在最窄“颈部”处）的自由能过小而无法控制其稳
定性，致使波动现象出现；当液桥体积增大时，其表面自由能亦随之增大，从而使这种波动现象逐
渐消失（4.2 节的图 12（b）—（d）可佐证）。
不仅如此，为从试验角度研究湿颗粒间不同体积液桥（液桥体积亦较小， V LB ≤1×10 ）的毛细力
∗
-3
随颗粒间距的变化特征，Rabinovich 等 ［16］ 利用原子力显微镜（AFM）测定了 3 对玻璃质球体湿颗粒被液
体不完全浸润（θ =10°）时其间形成的液桥（液体选取石蜡油，其表面张力为 27.5×10 N/m）在不同颗粒
-3
间距对应的毛细力，其中 R R ≈1.84、1.71 和 1.44； V ∗ ≈1.3×10 、8.7×10 和 3.2×10 ；相应的试
-4
-5
-5
1 2 LB
*
*
*
验编号分别为①、②和③。整理这 3 对不等径球体湿颗粒间液桥取不同 d d 时 F 的实测值及式
r
（47）的预测值如图 8 所示，式（47）对试验①、②、
*
③中液桥 F 的预测值与其实测值较为吻合，预测
*
误差不超过 9%，仅当 d ≥ 0.5d 时，预测误差虽
∗
r
*
有所增大，但此时 F 已很小，与图 7 所示预测结
果类似。
当 给 定 V LB 、 2d、 θ 和 颗 粒 半 径（ R 和 R ）
2
1
时，则可依据椭圆弧假定按照如下方法计算不等径
湿颗粒间小体积液桥（V LB ≤1×10 ） 的 F：① 检查
∗
-3
2d 是否小于式（46）所确定的 2d ；② 依据式（42）
r
由确定的 V LB 和 d 计算 y ；③ 将 y 代入式（38）和
c2
c2
式（4），分别计算得 d 和 x ；④ 采用式（21）和式 *
∗
2 c2 图 8 R R 和 d ∗ d 不同时 F 的实测值及式（47）的
1 2 r
（27）分别得到 χ 和 η ；⑤ 联立式（47）和式（10）即
2 2 预测值（θ =10°）
— 453 —