Page 104 - 2021年第52卷第8期

y 方向上的达西流速 V 的解析解为：
y
)
ì Zone 1：V = -K [ 10xcos(10xy - 4x y 3 ]
3
ï y y
ï
)
í ì é(2y + 9 x ù 3æ 2y + 9 ö 3 ù （16）
ï
ïZone 2：V = -K í x cosê ê ú-0.4 x ç ÷ ú
ú
ï y 2y ï ë 2 û è 20 ø ú
î î û
本例中，MSFEM-D 先将研究区剖分为 1800（30×30×2）个三角形粗网格单元，再将每个粗网格剖
分为 9（3×3）个三角形细网格单元，即总计 16 200 个细网格单元；Model-Zhou-F、Model-Yeh-F 直接
将研究区剖分 16 200（90×90×2）个网格单元。
如 前 所 述 ， MSFEM-D 应 用 MSFEM 直 接 在 研 究 区 内 计 算 全 局 水 头 ， 而 Model-Zhou-F、 Mod⁃
el-Yeh-F 均使用 FEM-F 进行全局水头模拟，FEM-F 的网格剖分与 Model-Zhou-F、Model-Yeh-F 一
致 。 MSFEM-D 和 FEM-F 在 本 例 都 能 获 得 很 高 的 水 头 计 算 精 度 ， 全 局 平 均 误 差 分 别 为 0.079% 和
0.024%。
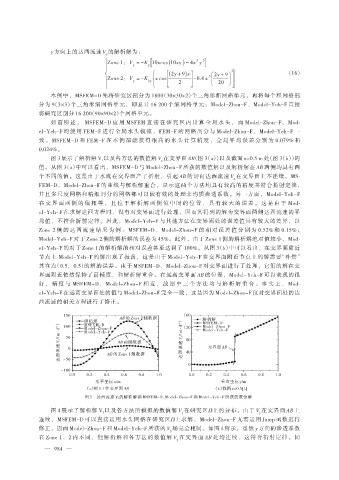
图 3 展示了解析解 V x以及各方法的数值解 V 在交界面 AB（图 3（a））以及截面 x=0.5 m 处（图 3（b））的
x
值。从图 3（a）中可以看出，MSFEM-D 与 Model-Zhou-F 所获的数值解以及解析解在 AB 两侧均具有两
个不同的值。这是由于水流在交界面产了折射，引起 AB 的切向达西流速 V 在交界面上不连续。MS⁃
x
FEM-D、Model-Zhou-F 的曲线与解析解重合，显示这两个方法均具有较高的精度并符合折射定律，
并且多尺度网格和精细剖分的网格都可以较有效的处理非均质渗透系数。另一方面，Model-Yeh-F
在 交 界 面 两 侧 的 值 相 等 ， 且 位 于 解 析 解 两 侧 值 中 间 的 位 置 ， 具 有 较 大 的 误 差 。 这 是 由 于 Mod⁃
el-Yeh-F 在求解达西方程时，没有对交界面进行处理，因而其得到的解为交界面两侧达西流速的平
均值，不符合折射定律。因此，Model-Yeh-F 与其他方法在交界面处的误差值具有较大的差异，以
Zone 2 侧 的 达 西 流 速 结 果 为 例 ： MSFEM-D、 Model-Zhou-F 的 相 对 误 差 值 分 别 为 0.52% 和 0.15% ；
Model-Yeh-F 对于 Zone 2 侧的解析解的误差为 45%。此外，由于 Zone 1 侧的解析解绝对值较小，Mod⁃
el-Yeh-F 的对于 Zone 1 的解析解的相对误差甚至达到了 100%。从图 3（b）中可以看出，在交界面附近
节点上 Model-Yeh-F 的解出现了振荡，这是由于 Model-Yeh-F 在交界面附近节点上的解需要“补偿”
其在点（0.5，0.5）的解的误差。由于 MSFEM-D、Model-Zhou-F 对交界面进行了处理，它们的解在交
界面附近依然保持了高精度，和解析解重合。在远离交界面 AB 的位置，Model-Yeh-F 可以表现的很
好 ， 精 度 与 MSFEM-D、 Model-Zhou-F 相 近 ， 故 图 中 三 个 方 法 均 与 解 析 解 重 合 。 事 实 上 ， Mod⁃
el-Yeh-F 在远离交界面处的值与 Model-Zhou-F 完全一致，这是因为 Model-Zhou-F 仅对交界面处的达
西流速的相关方程进行了修正。

150 AB 的 Zone 2 侧数据 160
解析解 解析解
MSFEM-D
（m · d -1 ） 100 Model-Zhou-F （m · d -1 ） 120 Model-Zhou-F
MSFEM-D
Model-Yeh-F
Model-Yeh-F
50
达西流速 V x/ 0 AB 的 Zone 1 侧数据 达西流速 V x/ 40 交界面 AB
80
AB 两侧数据
-50
0
-100
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
水平坐标 x/m 垂直坐标 y/m
（a）例 3.1 中交界面 AB （b）截面 x=0.5[L]
图 3 达西流速 V x的解析解和 MSFEM-D、Model-Zhou-F 和 Model-Yeh-F 所获的数值解
图 4 展示了解析解 V y 以及各方法所模拟的数值解 V 在研究区Ω上的分布。由于 V 在交界面 AB 上
y
y
连续，MSFEM-D 可以直接运用水头网格在研究区Ω上求解，Model-Zhou-F 无需运用 Jump 函数进行
修正，因而 Model-Zhou-F 和 Model-Yeh-F 所获的 V 场完全相同。如图 4 所示，虽然 y 方向的渗透系数
y
在 Zone 1、2 内不同，但解析解和各方法的数值解 V 在交界面 AB 处均连续，这符合折射定律。同
y
— 984 —