Page 17 - 水利学报2021年第52卷第11期

3.0 2.4 1.2

损伤值曲线
应力曲线
2.5 2.0 1.0

2.0 1.6 0.8
应力×10 6 /Pa 1.5 裂纹分形维曲线 1.2 裂纹分形维 0.6 损伤值

1.0 0.8 0.4
单元尺寸 1.0mm
单元尺寸 1.5mm
0.5 0.4 0.2
单元尺寸 2.0mm
单元尺寸 2.5mm
单元尺寸 3.0mm
0.0 0.0 0.0
0.0 1.0 2.0 3.0 4.0 5.0 6.0
应力×10 -4
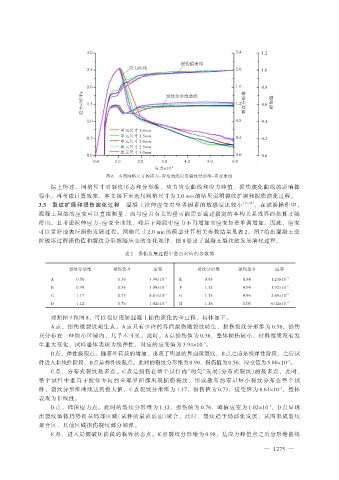
图 6 不同网格尺寸的应力-应变曲线以及裂纹分形维-应变曲线
综上所述，网格尺寸对裂纹形态和分形维、应力应变曲线和应力峰值、损伤演化曲线的影响都
很小，再考虑计算效率，本文接下来选用网格尺寸为 2.0 mm 的结果说明裂纹扩展和损伤演化过程。
3.3 裂纹扩展和损伤演化过程 混凝土拉伸应变对外界因素的敏感度比较小 ［37-38］ ，在试验操作中，
混凝土局部的应变可以直接测量，而与应力有关的量可能需要通过假定的本构关系或界面换算才能
得出。且考虑拉伸应力-应变全曲线，峰后下降段中应力不再增加而应变却是单调增加。因此，应变
可以更好地表征损伤发展过程。网格尺寸 2.0 mm 的模型计算相关参数结果见表 2。图 7 给出混凝土受
拉破坏过程损伤值和裂纹分形维随应变的变化规律，图 8 给出了混凝土裂纹的发展演化过程。

表 2 损伤发展过程中各点对应的参数值

裂纹分形维 损伤值 D 应变 裂纹分形维 损伤值 D 应变

A 0.58 0.36 3.94×10 -5 E 0.98 0.84 1.23×10 -4
B 0.90 0.56 5.00×10 -5 F 1.12 0.94 1.92×10 -4
C 1.17 0.73 8.61×10 -5 G 1.15 0.96 2.69×10 -4
D 1.12 0.76 1.02×10 -4 H 1.16 1.00 6.02×10 -4

对照图 7 和图 8，可以很好理解混凝土损伤演化的全过程，具体如下。
A 点，损伤微裂纹萌生点。A 点只有少许的界面损伤微裂纹萌生，损伤裂纹分形维为 0.58，损伤
只分布在一些细小区域内，几乎不可见。此时，A 点损伤值为 0.36，整体损伤较小，材料性质没有发
生重大变化，试样整体表现为线弹性，对应的应变值为 3.94×10 。
-5
B点，弹性极限点。随着外荷载的增加，出现了明显的界面微裂纹，B点之前是线弹性阶段，之后试
件进入非线性阶段，B点是弹性极限点。此时的裂纹分形维为 0.90，损伤值为 0.56，应变值为 5.00×10 。
-5
C 点，分布式裂纹最多点。C 点是损伤在整个试件内“均匀”发展（分布式裂纹）的最多点，此时，
整个试件中垂直于拉伸方向的全部界面都出现损伤裂纹，形成散布的零星短小裂纹分布在整个试
件，裂纹分形维曲线达到极大值，C 点裂纹分形维为 1.17，损伤值为 0.73，应变值为 8.61×10 ，整体
-5
表现为非线性。
D 点，峰值应力点。此时的裂纹分形维为 1.12，损伤值为 0.76，峰值应变为 1.02×10 ，D 点呈现
-4
出裂纹整体趋势向某局部区域（试件的最薄弱面）聚合。此时，裂纹趋于局部化发展，试图形成裂纹
聚合区，其他区域损伤裂纹部分回弹。
E 点，进入局部破坏阶段的临界状态点。E 点裂纹分形维为 0.98，是应力峰值点之后分形维曲线

— 1275 —