Page 88 - 2022年第53卷第3期

平衡法原理，能够联系工程的安全临界状态，但其分析结果对材料物理参数的分布极为敏感，易受
参数不确定性影响；同时受试验条件限制，难以反映物理参数实时动态演变引起边坡风险率实时变
化的特征。另一方面，利用边坡原位监测资料开展回归分析和预警指标拟定能够反映工程安全的实
时动态特征，但主流置信区间法的置信带宽度取值具有主观性，未能联系实际工程的安全临界状
态，属于统计意义上的经验值，限制了方法的使用。为了弥补以上不足，本文在传统置信区间法的
基础上构建了一个风险率函数，结合可靠度风险率可将边坡安全监测实测值直接转化为边坡的实时
风险率：
假设边坡监测序列{ }，i=1，2，…，n，分别输入对应的库水位{ }、降雨量{ }、温度{ }、时
X i
T i
H i
P i
刻{ }和测点坐标 x、y、z，建立边坡监测效应量的时空回归模型。根据回归模型残差服从正态分布的
θ i
̂
假定 ［16］ ，构造 μ = X ，σ = S 的正态分布曲线，如图 2 所示，可得到测点的测值 X 在不同区间的分布概
i
i
̂
率φ（X）。因此结合正态分布的概率密度函数，运用测点的实测值 X 和模型拟合值X ，结合式（9）构建
i
i
i
′
该测点测值的实时风险率P f ：
é ̂ ) 2 ù
X ̂ + | X ̂ - X | ê ( X - X i ú
i
X
φ ( ) = i i i 1 expê - údX i （12）
ú
ê
i
 ̂ - | X ̂ - X
X
i i i | 2π S ê 2S 2 ú
ë û
X
′
P = F [ φ ( )，P ] （13）
f i f
̂ ′
式中：X 为时刻 i 的测点实测值；X 为时刻i 对应的模型拟合值；S 为时空回归统计模型的标准差；P f
i
i
为构建的实时风险率；φ（X）为测值 X 的区间分布概率；F 为与φ（X）、P 有关的函数。
f
i
i
i
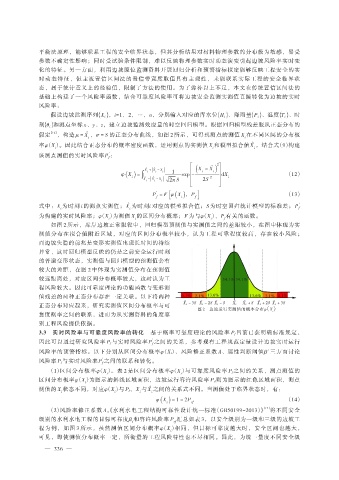
如图 2 所示，库岸边坡正常服役中，回归模型预测值与实测值之间的差距较小，在图中体现为实
测值分布在拟合值附近区域，对应的区间分布概率较小，认为工程可靠程度较高，存在较小风险；
而边坡失稳的前兆是变形实测值出现长时间的持续
异常，这时回归模型反映的仍是之前安全运行时刻
的普遍变形状态，实测值与回归模型的预测值会有
较大的差距，在图 2 中体现为实测值分布在预测值
较远距离处，对应区间分布概率较大，这时认为工 34.1% 34.1%
程风险较大。因此可靠度理论的功能函数与变形测
值残差的两种正态分布存在一定关联。以下将两种 0.1% 2.1% 13.6% 13.6% 2.1% 0.1%
̂
̂
̂
̂
̂
̂
X i - 3S X i - 2S X i - S X i ̂ X i + S X i + 2S X i + 3S
正态分布对应起来，研究实测值区间分布概率与可
图 2 边坡运行实测值的概率分布φ（X）
i
靠度概率之间的联系，进而为从实测资料的角度鉴
别工程风险提供依据。
3.3 实时风险率与可靠度风险率的转化 基于概率可靠度理论的风险率 P f 目前已获明确标准规定，
′
因此可以通过研究风险率 P f与实时风险率P f 之间的关系，参考现有工程规范定量设计边坡实时运行
风险率的预警指标。以下分别从区间分布概率φ（X i ）、风险修正系数 A、属性判断阈值β′ 三方面讨论
′
风险率 P f与实时风险率P f 之间的联系和转化。
（1）区间分布概率φ（X）。表 2 是区间分布概率φ（X）与可靠度风险率 P f之间的关系，测点测值的
i
i
区间分布概率φ（X）为图示的斜线区域面积，边坡运行容许风险率 P rf则为图示的红色区域面积，测点
i
̂
测值的 X 状态不同，对应φ（X）与 P f、X 与X 之间的关系式不同。当测值处于临界状态时，有：
i
i
i
i
φ ( ) = 1 - 2P rf （14）
X
i
［17］
（2）风险率修正系数 A。《水利水电工程结构可靠性设计统一标准（GB50199-2013）》 将不同安全
级别的水利水电工程的目标可靠度β 和容许风险率 P 汇总如表 3，以安全级别为一级和三级的边坡工
t
rf
程为例，如图 3 所示，虽然测值区间分布概率φ（X）相同，但目标可靠度越大时，安全区间也越大，
i
可见，即使测值分布概率一定，所衡量的工程风险特性也不尽相同。因此，为统一量度不同安全级
— 336 —