Page 101 - 2022年第53卷第4期

时，上游流量变化量Δq in ( ) k 在 k+1 时刻已影响到最下游水位，且影响的时长为T s - τ d ，因此在计算
) )
e (k + 1 - e ( ) k 时，应该用Δq in ( ) k 而非Δq in (k - 1 )进行计算，且Δq in ( ) k 乘以的时段长为T s - τ d ；而Δe (k + 1
含 义 为 k + 1 瞬 时 的 水 位 变 化 率 持 续 一 个 调 控 间 隔 时 间 下 的 水 位 变 化 量 ， 则 为 Δq in ( ) k 及 出 流
Δq out ( ) k 和Δq offtake ( ) k 持续影响T s 时段长带来的变化量，因此Δe (k + 1 )的计算用Δq in ( ) k 乘以T s 。按照此思
路，本文采用以下模型来对积分时滞模型（4）进行离散：

)
)
e (k + 1 - e ( ) k = De ( ) k + (n + 1 )T - τ d Dq (k - n - T s [Dq ( ) k + Dq ( ] ) k （10）
s
A in A out offtake
d d
T T
)
)
De (k + 1 = De ( ) k + s Dq (k - n - s [Dq ( ) k + Dq ( ] ) k （11）
A in A out offtake
d d
式中 n 为整数，且满足n < τ T ≤ n + 1。
d s
4 计算实例
4.1 研究渠池 本文选择南水北调中线干线工程的最后 6 段串联渠池为研究对象，通过构造此渠池
系统的仿真模型来模拟在预测控制下的渠池状态。仿真模型采用本文自主开发的水动力模型仿真平
台 ［25］ 来构建；在水动力模型仿真平台中，闸门各个调控时刻的开度调整值由预测模型决定。研究渠
池全长 112 km，明渠断面都为梯形断面，每个渠池末端有分水口向用水户供水，各渠池的特征参数
及初始流量值见表 1 所示。假设渠池系统上、下游分别为水深 7 m 和 3 m 的水位边界，初始时刻输水
系统为稳定状态，各控制点水位都稳定在目标水位。在工程的实际调控中，各渠池控制点水位并不
严格要求稳定在目标水位上，控制点水位可以在目标水位±0.1 m 的范围内波动。这是因为工程中，
各个渠池的水深平均在 4 m 以上，±0.1 m 的水位波动情况下，节制闸和分水口的过水流量的变化相对
比较小，可认为供水量相对稳定，因此工程中对于±0.1 m 范围内的水位偏差的调控较少，来降低闸
门的调控次数。

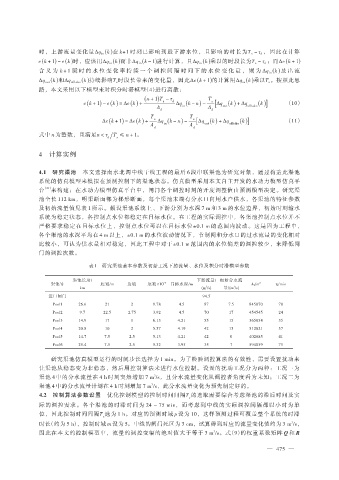
表 1 研究渠池基本参数及初始工况下的流量、水位及积分时滞模型参数

渠池长度/ 下游流量/ 初始分水流
渠池号 底宽/m 边坡 底坡×10 -5 目标水深/m A d/m 2 τ d/min
3
3
km (m /s) 量/(m /s)
进口闸门 94.5
Pool1 26.6 21 2 9.78 4.5 87 7.5 845070 70
Pool2 9.7 22.5 2.75 3.92 4.5 70 17 454545 24
Pool3 14.9 17 1 6.13 4.21 55 15 365854 35
Pool4 20.8 10 2 5.37 4.19 42 13 512821 57
Pool5 14.7 7.5 2.5 5.13 4.21 42 0 402685 41
Pool6 25.4 7.5 2.5 5.32 3.95 35 7 594059 75

研究渠池仿真模型运行的时间步长选择为 1 min。为了检验调控算法的有效性，需要设置扰动来
让渠池从稳态变为非稳态，然后用控制算法来进行水位控制。设置的扰动工况分为两种：工况一为
渠池 4 中的分水流量在 4 h 时刻突然增加 7 m /s，且分水流量变化从调控者角度看为未知；工况二为
3
渠池 4 中的分水流量计划在 4 h 时刻增加 7 m /s，此分水流量变化为预先制定好的。
3
4.2 控制算法参数设置 优化控制模型的控制时间间隔T 的选取需要综合考虑渠池的滞后时间及实
s
际的调控需求。各个渠池的时滞时间为 24 ~ 75 min，而考虑到中线的实际调控间隔都以小时为单
位，因此控制时间间隔T 选为 1 h。对应的预测时域 p 设为 10，这样预测过程可覆盖整个系统的时滞
s
时长（约为 5 h），控制时域 m 设为 5。中线的闸门死区为 3 cm，试算得到对应的流量变化值约为 3 m /s，
3
因此在本文的控制模型中，流量的调控变幅的绝对值大于等于 3 m /s。式（9）的权重系数矩阵 Q 和 R
3

— 475 —