Page 100 - 2022年第53卷第8期

ｇｄＨ ｄ ｖ ｆｖｖ
ｍ
＋ ＋ ＝ ０
ａ ｄｔ ｄｔ ２Ｄ
Ｃ ＋ ｍ （１２）
ｄｘ
＝＋ ａ
ｄｔ ｍ
ｇｄＨ ｄｖ ｆｖｖ
ｍ
－ ＋ ＋ ＝ ０
ａ ｄｔ ｄｔ ２Ｄ
ｍ
Ｃ － （１３）
ｄ ｘ
＝－ ａ
ｄｔ ｍ
引入管路截面面积 Ａ与含沙水流量 Ｑ表征混合物流速 ｖ，对特征线方程进行积分，令 ｖ ＝ Ｑ?Ａ，Ｂ ＝
２
ａ ?ｇＡ，Ｒ ＝ ｆΔ ｘ?２ｇＤＡ 得到差分形式的代数方程如下：
ｍ
ｍ
＋
Ｃ ：Ｈ ＝ Ｈ － Ｂ（Ｑ － Ｑ ） － ＲＱ Ｑ ＝ ０ （１４）
Ａ
Ｐ
Ａ
Ｐ
Ａ
Ａ
－
Ｃ ：Ｈ ＝ Ｈ ＋ Ｂ（Ｑ － Ｑ ） ＋ ＲＱ Ｑ ＝ ０ （１５）
Ｐ
Ｂ
Ｂ
Ｂ
Ｂ
Ｐ
在方程（ １４）和方程（１５）的基础上引入边界条件与水力元件代数方程，即可求解得到特定时间位置
参数 Ｐ点的压力 Ｈ 与流量 Ｑ 的数值解。
Ｐｉ Ｐｉ
３ 理论分析
３．１ 清水模型验证 现以 Ｂｅｒｇａｎｔ等 ［２２］ ＲＰＶ系统（水箱－ 管路－ 阀门）的清水关阀水锤实验数据为参考，
采用前节所述含沙水锤数值计算特征线方法进行关阀瞬变流分析。该实验包含高为 ３２ｍ的上游水箱，
通过长度为 ３７．２ｍ、直径为 ０．０２２ｍ的管道连接至末段阀门，管道清水条件下的糙率 ｎ为 ０．０３７。在初
始流速 ｖ为 ０．３ｍ?ｓ、关阀时间为 ０．００９ｓ的实验条件下，测量得到了管道末端与中点的清水水锤瞬态
０
３
＝ ２６５０ｋｇ?ｍ 的泥沙颗粒，
压力数据。为了更好地对比清水水锤与含沙水锤的数值计算结果，针对 ρ ｍ
３
在颗粒直径 ｄ＝ ０．０１～０．５ｍｍ、含沙量 Ｓ ＝ １～１００ｋｇ?ｍ 的范围内，选取三组不同参数介质（其中一组为
ｓ
３
清水，即含沙水颗粒参数设定为 Ｓ ＝ ０ｋｇ?ｍ ，ｄ＝ ０ｍｍ ）进行对比分析如图 １所示。此外，由于含沙水
ｓ
与清水的密度不同，本文将含沙水压力水头 Ｈ 统一换算至清水压力水头 Ｈ ，其表达式如下：
ｗ
ｍ
Ｈ ］Ｈ
ρ ｍ ｍ ［Ｓ ＋ （１ － Ｓ? ρ ｓ ）·ρ Ｌ ｍ
Ｈ ＝ ＝ （１６）
ｗ
ρ Ｌ ρ Ｌ
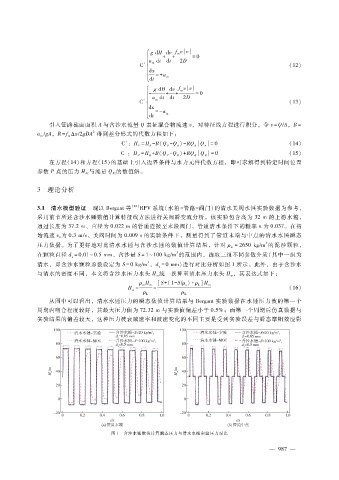
从图中可以看出，清水水锤压力的瞬态数值计算结果与 Ｂｅｒｇａｎｔ实验数据在水锤压力波的第一个
周期内吻合程度较好，其最大压力值为 ７２．３２ｍ与实验值偏差小于 ０．５％；而第一个周期后仿真数据与
实验结果的偏差较大，这种压力波衰减速率和波速变化的不同主要是受到实验误差与瞬态摩阻效应影

图 １ 含沙水锤数值计算瞬态压力与清水水锤实验压力对比

— ９ ８ ７ —