Page 101 - 2022年第53卷第8期

３
响。对于另外两组泥沙而言，Ｓ ＝ ２０ｋｇ?ｍ ，ｄ＝ ０．０５ｍｍ时计算得到的最大瞬态压力为 ７３．４５ｍ，较清
ｓ
３
水水锤高出 １．５５％；而 Ｓ ＝ １００ｋｇ?ｍ ，ｄ＝ ０．５ｍｍ时最大压力值为 ７７．９１ｍ，较清水高出 ７．７１％。对于
ｓ
最小压力值而言，含沙水锤与清水水锤数值计算结果的偏差量小于 １．６２ｍ，较最大压力而言偏差较
小。无论是管道末端还是中点的含沙水锤压力波动规律与清水仿真一致，其波速存在一定的偏差但差
别较小。可以看出，低含沙量、低颗粒直径的含沙水锤压力与清水水锤更为接近，而与高含沙量、高
颗粒直径的偏差较大。这一方面论证了含沙水锤数值计算结果随颗粒浓度和直径变化趋势的合理性，
另一方面说明了一定规模的颗粒存在对于含沙管路水锤压力产生一定的影响，需要进一步具体地分析
不同的颗粒参数对含沙水锤过程压力波动的影响。
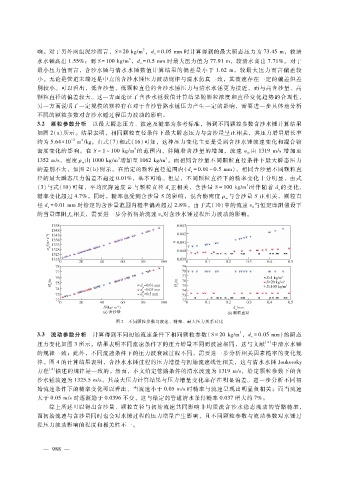
３．２ 颗粒参数分析 以最大瞬态压力、波速及糙率为参考标准，得到不同颗粒参数含沙水锤计算结果
如图 ２（ａ）所示。结果表明，相同颗粒直径条件下最大瞬态压力与含沙量呈正相关，其压力增量增长率
－ ２ ４
约为 ５．６４ × １０ ｍ ?ｋｇ。由式（７）和式（１６）可知，这种压力变化主要是受到含沙水锤波速变化和混合物
３
密度变化的影响。在 Ｓ ＝ １～１００ｋｇ?ｍ 的范围内，伴随着含沙量的增加，波速 ａ 由 １３１９ｍ?ｓ增加至
ｍ
３
３
由 １０００ｋｇ?ｍ 增加至 １０６２ｋｇ?ｍ 。而相同含沙量不同颗粒直径条件下最大瞬态压力
１３５２ｍ?ｓ，密度 ρ ｍ
的差别不大，如图 ２（ｂ）所示。在给定的颗粒直径范围内（ｄ＝ ０．０１～０．５ｍｍ），相同含沙量不同颗粒直
ｓ
径的最大瞬态压力偏差不超过 ０．０１％，基本可略。但是，不同颗粒直径下的糙率变化十分明显，由式
ω与颗粒直径 ｄ正相关，含沙量 Ｓ ＝ １００ｋｇ?ｍ 时伴随着 ｄ的变化，
（３）与式（１０）可知，平均沉降速度 珚 ｓ ３ ｓ
与含沙量 Ｓ正相关，颗粒直
糙率变化超过 ４．７％。同时，糙率也受到含沙量 Ｓ的影响，混合物密度 ρ ｍ
径 ｄ＝ ０．０１ｍｍ时给定的含沙量范围内糙率偏差超过 ２．８％。由于式（１０）中的流速 ｖ与恒定摩阻假设下
０
ｓ
的当量摩阻 ｆ相关，需要进一步分析初始流速 ｖ对含沙水锤过程压力波动的影响。
ｍ ０

图 ２ 不同颗粒参数与波速、糙率、最大压力关系对比

３
３．３ 流动参数分析 计算得到不同初始流速条件下相同颗粒参数（Ｓ ＝ ２０ｋｇ?ｍ ，ｄ＝ ０．０５ｍｍ ）的瞬态
ｓ
压力变化如图 ３所示。结果表明不同流速条件下的压力增量不同而波速相同，这与文献 ［４］ 中清水水锤
的规律一致；此外，不同流速条件下的压力波衰减过程不同，需要进一步分析相关因素糙率的变化规
律。图 ４的计算结果表明，含沙水水锤过程的压力增量与初始流速线性相关，这与清水水锤 Ｊｏｕｋｏｖｓｋｙ
方程 ［４］ 描述的规律是一致的。然而，本文给定管路条件的清水波速为 １３１９ｍ?ｓ，给定颗粒参数下的含
沙水锤波速为 １３２５．５ｍ?ｓ，其最大压力计算结果与压力增量变化率存在明显偏差。进一步分析不同初
始流速条件下的糙率变化可以看出，当流速小于 ０．０５ｍ?ｓ时糙率与流速呈现出明显负相关；而当流速
大于 ０．０５ｍ?ｓ时逐渐趋于 ０．０３９６不变，这与给定的管道清水条件糙率 ０．０３７增大约 ７％。
综上所述可以得出含沙量、颗粒直径与初始流速共同影响非均质流含沙水稳态流动的管路糙率，
而初始流速与含沙量同时也会对水锤过程的压力增量产生影响，且不同颗粒参数与流动参数对水锤过
程压力波动影响的程度和相关性不一。

８
— ９ ８ —