Page 70 - 2022年第53卷第10期

峡水库泥沙淤积量平衡值的计算公式。吕宜卫等 ［６］
在推导下荆江河段单位河长累计冲刷量平衡值计算
公式时，在考虑挟沙强度和汛期来沙量影响的基础
上，引入了无量纲水面比降来减弱洞庭湖顶托效应
对模型计算的影响。郑珊 ［７］ 将扰动后河道淤积体的
平衡纵剖面形态概化为三角形或梯形，为累计淤积
量平衡值的计算提供了一种概化方法。调整速率参
数 β 多取为常数，仅少数研究在模拟黄河下游平滩
流量时，把调整速率参数 β表示为汛期平均流量的
幂函数 ［８］ 。
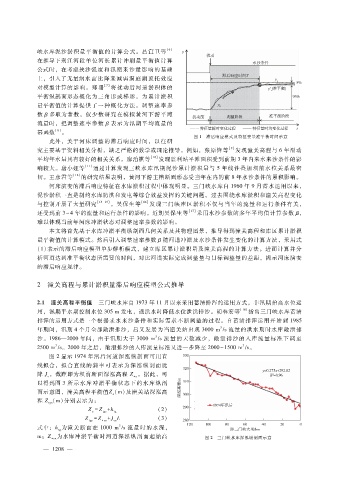
图 １ 滞后响应模式及特征变量准平衡时间示意
此外，关于河床调整的滞后响应时间，以往研
究主要基于资料相关分析，缺乏严格的数学或理论推导。例如，张原锋等 ［９］ 发现潼关高程与 ６年滑动
平均年水量具有较好的相关关系。廖治棋等 ［１０］ 发现监利站平滩面积受到前期 ３年内来水来沙条件的影
响较大。唐小娅等 ［１１］ 通过计算发现三峡水库汛期泥沙累计淤积量与 ５年线性叠加坝前水位关系最密
切。王彦君等 ［１２］ 的研究结果表明，黄河下游主槽断面形态受当年在内的前 ８年水沙条件的累积影响。
河床演变的滞后响应特征在水库淤积过程中体现明显。三门峡水库自 １９６０年 ９月蓄水运用以来，
泥沙淤积一直是制约水库防洪和发电等综合效益发挥的关键问题。过去围绕水库淤积和潼关高程变化
与控制开展了大量研究 ［１３ － １５］ 。吴保生等 ［１６］ 发现三门峡库区淤积不仅与当年的流量和运行条件有关，
还受到前 ３～４年的流量和运行条件的影响。近期吴保生等 ［１７］ 采用水沙参数的多年平均值计算参数 β ，
难以体现当前年河床冲淤状态对调整速率参数的影响。
本文将首先基于水库冲淤平衡纵剖面几何关系及其物理图景，推导得到潼关高程和库区累计淤积
量平衡值的计算模式。然后引入调整速率参数 β 随河道冲淤及水沙条件发生变化的计算方法，采用式
（ １）表示的滞后响应模型单步解析模式，建立库区累计淤积量及潼关高程的计算方法。进而计算并分
析河道达到准平衡状态所需要的时间，对比河道实际完成调整量与目标调整量的差距，揭示河床演变
的滞后响应规律。

２ 潼关高程与累计淤积量滞后响应模型公式推导

２．１ 潼关高程平衡值 三门峡水库自 １９７３年 １１月以来采用蓄清排浑的运用方式，非汛期抬高水位运
用，汛期平水期控制水位 ３０５ｍ发电，遇洪水时降低水位泄洪排沙。胡春宏等 ［１８］ 指出三门峡水库蓄清
排浑的运用方式是一个根据来水来沙条件和实际需求不断调整的过程。自蓄清排浑运用开始到 １９８５
３
年期间，汛期 ４个月全部敞泄排沙，后又发展为当潼关站出现 ３０００ｍ ?ｓ流量的洪水期时水库敞泄排
３
沙。１９８６—２０００年间，由于汛期大于 ３０００ｍ ?ｓ流量的天数减少，敞泄排沙的入库流 量标 准下调至
３
３
２５００ｍ ?ｓ。２０００年之后，敞泄排沙的入库流量标准又进一步降至 ２０００～１５００ｍ ?ｓ。
图 ２显示 １９７４年汛后河道深泓纵剖面可用直
线拟合，拟合直线的斜率可表示为深泓纵剖面比
降 Ｊ，截距即为坝前断面深泓高程 Ｚ 。据此，可
ｓ ｓ
以得到图 ３所示水库冲淤平衡状态下的水库纵剖
面示意图，潼关高程平衡值Ｚ（ｍ）及潼关站深泓高
ｅ
程 Ｚ （ｍ）分别表示为：
ｔｇｓ
Ｚ ＝ Ｚ ＋ ｈ ｔｇ （２）
ｅ
ｔｇｓ
Ｚ ＝ Ｚ ＋ ＪＬ （３）
ｔｇｓ ｅｓ ｅｓ
３
式中：ｈ为潼关断面在 １０００ｍ ?ｓ流量时的水深，
ｔｇ
ｍ；Ｚ 为水库冲淤平衡时河道深泓纵剖面起始高
ｅｓ 图 ２ 三门峡水库深泓纵剖面示意
— １ ２ ８ —
０