Page 73 - 2022年第53卷第10期

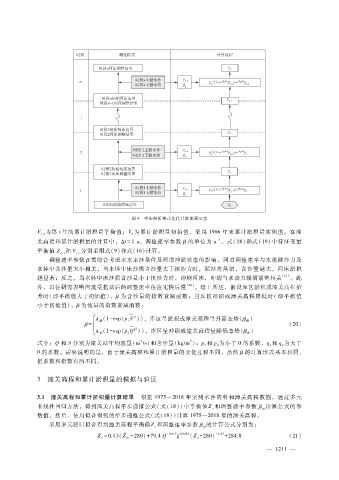
图 ４ 单步解析模式迭代计算流程示意
Ｖ 为第 ｉ年的累计淤积量平衡值；Ｖ为累计淤积量初始值，采用 １９６６年末累计淤积量实测值。在潼
ｅ，ｉ ０
－ １
关高程和累计淤积量的计算中，Δ ｔ ＝ １ａ ，调整速率参数 β 的单位为 ａ 。式（１８）和式（１９）中特征变量
平衡值 Ｚ 和 Ｖ 分别采用式（９）和式（１６）计算。
ｅ，ｉ
ｅ，ｉ
调整速率参数 β 需综合考虑来水来沙条件及河道冲淤状态的影响。河道调整速率与水流挟沙力及
水体中含沙量大小相关，当水体中床沙质含沙量大于挟沙力时，泥沙将落淤，含沙量越大，河床淤积
越显著；反之，当水体中床沙质含沙量小于挟沙力时，冲刷河床，冲刷与水动力强弱紧密相关 ［２１］ 。此
外，以往研究表明河流受扰动后的调整速率往往先快后慢 ［２２］ 。综上所述，假设库区淤积或潼关高程抬
升时（即平衡值大于初始值），β 为含沙量的指数衰减函数；当库区冲刷或潼关高程降低时（即平衡值
小于初始值），β 为流量的指数衰减函数：

{ λ 淤 （１ － ｅｘｐ（ｐＳ ）），库区呈淤积或潼关高程呈升高态势（ β 淤 ）
ｑ１
１
β ＝ （２０）
ｑ２
λ 冲 （１ － ｅｘｐ（ｐＱ ）），库区呈冲刷或潼关高程呈降低态势（ β 冲 ）
２
３
３
式中：Ｑ和 Ｓ分别为潼关站年均流量（ｍ ?ｓ）和含沙量（ｋｇ?ｍ ）；ｐ和 ｐ为小于 ０的系数，ｑ和 ｑ为大于
１ ２ １ ２
０的系数。需要说明的是，由于潼关高程和累计淤积量的变化过程不同，虽然 β 的计算形式基本相同，
但系数和指数有所不同。
３ 潼关高程和累计淤积量的模拟与验证

３．１ 潼关高程和累计淤积量计算结果 根据 １９７５—２０１８年实测水沙资料和潼关高程数据，通过多元
计算公式的参
非线性回归方法，得到潼关高程单步递推公式（式（ １８））中平衡值Ｚ和调整速率参数 β ｔｇ
ｅ
数值。然后，使用拟合得到的单步递推公式（式（１８））计算 １９７５—２０１８年的潼关高程。
的计算公式分别为：
ｅ
采用多元回归拟合得到潼关高程平衡值Ｚ和调整速率参数 β ｔｇ
＾
Ｚ ＝ ０ ．４３（ Ｚ － ２８０ ） ＋ ７９ ．４Ｑ － ０ ．０１９ ０．００２２ （Ｚ－ ２８０ ） － ０ ．２５ ＋ ２８４ ．８ （２１）
ξ
ｅ ｄ１ ｄ
２
— １ １ １ —