Page 77 - 2022年第53卷第10期

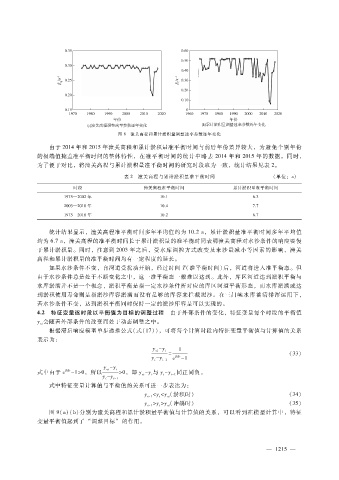
图 ８ 潼关高程和累计淤积量调整速率参数逐年变化

由于 ２０１４年和 ２０１５年潼关高程和累计淤积量准平衡时间与前后年份差异较大，为避免个别年份
的极端值掩盖准平衡时间的整体特性，在准平衡时间的统计中略去 ２０１４年和 ２０１５年的数据。同时，
为了便于对比，将潼关高程与累计淤积量准平衡时间的研究时段取为一致，统计结果见表 ２。
表 ２ 潼关高程与累计淤积量准平衡时间 （单位：ａ）

时段 潼关高程准平衡时间 累计淤积量准平衡时间
１９７５—２００２年 １０．１ ６．３
２００３ —２０１８年 １０．４ ７．７
１９７５—２０１８年 １０．２ ６．７

统计结果显示，潼关高程准平衡时间多年平均值约为 １０．２ａ，累计淤积量准平衡时间多年平均值
约为 ６．７ａ，潼关高程的准平衡时间长于累计淤积量的准平衡时间表明潼关高程对水沙条件的响应要慢
于累计淤积量。同时，注意到 ２００３年之后，受水库调控方式改变及来沙量减小等因素的影响，潼关
高程和累计淤积量的准平衡时间均有一定程度的延长。
如果水沙条件不变，自河道受扰动开始，经过时间 Ｔ（准平衡时间）后，河道将进入准平衡态。但
由于水沙条件总是处于不断变化之中，这一准平衡态一般难以达到。此外，库区河道达到淤积平衡与
水库淤满并不是一个概念，淤积平衡是指一定水沙条件所对应的库区河道平衡形态，而水库淤满或达
到淤积使用寿命则是指淤沙库容淤满而没有足够的库容来拦截泥沙。在三门峡水库蓄清排浑运用下，
若水沙条件不变，达到淤积平衡同时保持一定的淤沙库容是可以实现的。
４．２ 特征变量逐时段以平衡值为目标的调整过程 由于外部条件的变化，特征变量每个时段的平衡值
ｙ会随着外部条件的改变而处于动态调整之中。
ｅｉ
根据滞后响应模型单步递推公式（式（１７）），可将每个计算时段内特征变量平衡值与计算值的关系
表示为：
ｙ－ ｙ １
ｅｉ
ｉ
＝ （３３）
ｙ － ｙ βΔ ｔ
ｉ － １ ｅ － １
ｉ
ｙ－ ｙ ｉ
ｅｉ
βΔ ｔ
式中由于 ｅ － １＞０，所以 ＞０，即 ｙ－ ｙ与 ｙ － ｙ 同正同负。
ｉ
ｉ
ｉ － １
ｅｉ
ｙ － ｙ
ｉ － １
ｉ
式中特征变量计算值与平衡值的关系可进一步表达为：
ｙ ＜ｙ＜ｙ（淤积时） （３４）
ｉ － １ ｉ ｅｉ
ｙ ＞ｙ＞ｙ（冲刷时） （３５）
ｉ － １ ｉ ｅｉ
图 ９（ａ）（ｂ）分别为潼关高程和累计淤积量平衡值与计算值的关系，可以看到在模型计算中，特征
变量平衡值起到了 “调整目标” 的作用。
２
— １ １ ５ —