Page 78 - 2022年第53卷第10期

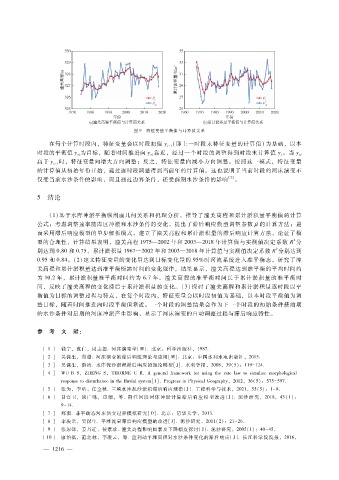
图 ９ 特征变量平衡值与计算值关系

在每个计算时段内，特征变量会以时段初值 ｙ （即上一时段末特征变量的计算值）为基础，以本
ｉ － １
时段的平衡值 ｙ为目标，随着时间推进向 ｙ靠近，经过一个时段的调整得到时段末计算值 ｙ。当 ｙ
ｉ
ｅｉ
ｅｉ
ｅｉ
高于 ｙ 时，特征变量向增大方向调整；反之，特征变量向减小方向调整。按照这一模式，特征变量
ｉ － １
的计算值从初始年份开始，通过逐时段调整得到当前年的计算值。这也说明了当前时段的河床演变不
仅受当前水沙条件的影响，而且通过边界条件，还受前期水沙条件的影响 ［２］ 。
５ 结论

（１）基于水库冲淤平衡纵剖面几何关系和机理分析，推导了潼关高程和累计淤积量平衡值的计算
公式；考虑调整速率随库区冲淤和水沙条件的变化，提出了滞后响应模型调整参数 β的计算方法；进
而采用滞后响应模型的单步解析模式，建立了潼关高程和累计淤积量的滞后响应计算方法，论证了模
２
型的合理性，计算结果表明，潼关高程 １９７５—２００２年和 ２００３—２０１８年计算值与实测值决定系数 Ｒ分
２
别达到 ０．８０和 ０．７５，累计淤积量 １９６７—２００２年和 ２００３—２０１８年计算值与实测值决定系数 Ｒ分别达到
０．９５和 ０．８４。（２）定义特征变量的变化量达到目标变化量的 ９５％时河流系统进入准平衡态，研究了潼
关高程和累计淤积量达到准平衡所需时间的变化规律，结果显示，潼关高程达到准平衡的平均时间约
为 １０．２年，累计淤积量准平衡时间约为 ６．７年。潼关高程的准平衡时间长于累计淤积量的准平衡时
间，反映了潼关高程的变化滞后于累计淤积量的变化。（３）探讨了潼关高程和累计淤积量逐时段以平
衡值为目标的调整过程与特点，在每个时段内，特征变量会以时段初值为基础，以本时段平衡值为调
整目标，随着时间推进向时段平衡值靠近。一个时段的调整结果会作为下一个时段的初始条件使前期
的水沙条件对后期的河床冲淤产生影响，显示了河床演变的自动调整过程与滞后响应特性。

参 考 文 献：

［ １］ 钱宁，张仁，周志德．河床演变学［Ｍ］．北京：科学出版社，１９８７．
［ ２］ 吴保生，郑珊．河床演变的滞后响应理论与应用［Ｍ］．北京：中国水利水电出版社，２０１５．
［ ３］ 吴保生，游涛．水库泥沙淤积滞后响应的理论模型［Ｊ］．水利学报，２００８，３９（５）：１１９ － １２４．
［ ４］ ＷＵＢ Ｓ， ＺＨＥＮＧ Ｓ， ＴＨＯＲＮＥ Ｃ Ｒ．Ａ ｇｅｎｅｒａｌｆｒａｍｅｗｏｒｋｆｏｒｕｓｉｎｇｔｈｅｒａｔｅｌａｗ ｔｏｓｉｍｕｌａｔｅｍｏｒｐｈｏｌｏｇｉｃａｌ
ｒｅｓｐｏｎｓｅｔｏｄｉｓｔｕｒｂａｎｃｅｉｎｔｈｅｆｌｕｖｉａｌｓｙｓｔｅｍ ［Ｊ］．ＰｒｏｇｒｅｓｓｉｎＰｈｙｓｉｃａｌＧｅｏｇｒａｐｈｙ，２０１２，３６（５）：５７５ － ５９７．
［ ５］ 张为，李昕，任金秋．三峡水库泥沙淤积滞后响应规律［Ｊ］．工程科学与技术，２０２１，５３（５）：１ － ８．
［ ６］ 吕宜卫，谈广 鸣，郑 珊，等．荆 江 河 段 河 床 冲 淤 计 算 滞 后 响 应 模 型 改 进 ［Ｊ］．泥 沙 研 究，２０１８，４３（１）：
９ － １４．
［ ７］ 郑珊．非平衡态河床演变过程模拟研究［Ｄ］．北京：清华大学，２０１３．
［ ８］ 李凌云，吴保生．平滩流量滞后响应模型的改进［Ｊ］．泥沙研究，２０１１（２）：２１ － ２６．
［ ９］ 张原锋，姜乃迁，侯素珍．潼关高程影响因素及下降幅度探讨［Ｊ］．泥沙研究，２００５（１）：４０ － ４５．
［１０］ 廖治棋，范北林，李凌云，等．监利站平滩面积对水沙条件变化的滞后响应［Ｊ］．长江科学院院报，２０１６，

— １ ２ ６ —
１