Page 71 - 2022年第53卷第10期

程，即坝前断面深泓高程，ｍ；Ｊ为水库冲淤平衡时河道深泓纵剖面比降；Ｌ为潼关断面至大坝的河
ｅｓ
流长度，取 １１３．５ｋｍ。
＾
考虑到 Ｚ 主要受上游来水来沙和下游水库运用水位的影响 ［１７］ ，Ｚ 可以表示成加权水位 Ｚ 的函
ｅｓ
ｄ１
ｅｓ
数，由变化项和常数项组成，公式如下：
＾
Ｚ ＝ Ｋ（ Ｚ － Ｚ ） ＋ Ｚ′ （４）
ｅｓ １ ｄ１ ｄｋ ｂ
式中：Ｚ 为三门峡大坝的底孔高程，即 ２８０ｍ；Ｋ为变化项系数，Ｚ′为常数项，两者均可通过率定得
ｄｋ
１
ｂ
＾
到；Ｚ 为年加权水位。参考吴保生等 ［２，１６］ 加权水位的计算方法，同时考虑含沙量的影响，年加权水位
ｄ１
＾
Ｚ 可表示为：
ｄ１
ｎ ｎ
＾
ε
ε
σ
Ｚ ＝ Ｑ ＳＺ ｄｉ∑ Ｑ Ｓ σ （５）
ｄ１ ∑
ｔｇｉ ｉ
ｔｇｉ ｉ
ｉ ＝１ ｉ ＝１
式中：Ｑ 为日均入库流量；Ｓ为日均入库含沙量；Ｚ 为日均坝前水位；ｎ为加权计算的天数，平年
ｉ
ｔｇｉ
ｄｉ
ｎ ＝ ３６５ ，闰年 ｎ ＝ ３６６ ；ε 和 σ分别为流量和含沙量的指数。
根据以往研究 ［１９ － ２０］ ，河道深泓纵剖面比降 Ｊ与水沙条件及水库运用水位相关，可表示为：
ｅｓ
ｃ１
ａ１ ｂ１
Ｊ ＝ ＫＱ ξ （Ｚ － Ｚ ） Ｊ （６）
０
ｄ１
ｄｋ
ｂ
ｅｓ
３
式中：Ｊ为 １９６０年 ９月水库投入运用时的初始河床比降，等于 ０．２８６‰；Ｑ为年均入库流量，ｍ ?ｓ；
０
６
ξ 为年均来沙系数，ｋｇ·ｓ?ｍ ；Ｚ 为年均坝前水位，ｍ。
ｄ１
将式（４）和式（６）代入式（３），得到 Ｚ 的表达式：
ｔｇｓ
＾
ｃ１
ａ１ ｂ１
Ｚ ＝ Ｋ（ Ｚ － Ｚ ） ＋ ＫＪＬＱ ξ （Ｚ－ Ｚ ） ＋ Ｚ′ （７）
ｔｇｓ １ ｄ１ ｄｋ ｂ ０ ｄ ｄｋ ｂ
进而将式（７）代入式（２），即可得到潼关高程平衡值Ｚ的完整表达式：
ｅ
＾
ｃ１
ａ１ ｂ１
Ｚ ＝ Ｋ （Ｚ － Ｚ ） ＋ ＫＪＬＱ ξ （Ｚ－ Ｚ ） ＋ Ｚ′ ＋ ｈ （８）
ｅ １ ｄ１ ｄｋ ｂ ０ ｄ ｄｋ ｂ ｔｇ
式（ ８）可进一步简化为：
＾
ａ１ ｂ１
ｃ１
(
Ｚ ＝ Ｋ（ Ｚ － Ｚ ） ＋ ＫＱ ξ Ｚ－ Ｚ ) ＋ Ｚ ｃ （９）
ｄｋ
ｄ１
ｄ
２
ｄｋ
１
ｅ
式中：Ｋ ＝ ＫＪＬ，Ｚ ＝ Ｚ′＋ ｈ，ａ、ｂ、ｃ为指数。考虑到比降与 Ｑ和 Ｚ成反比，而与 ξ 成正比，定
２ ｂ ０ ｃ ｂ ｔｇ １ １ １ ｄ
性上应有：ａ＜０，ｂ＞０，ｃ＜０。式（９）即为潼关高程平衡值的计算式。其中等号右边的第一项和第三
１ １ １
项相加为包含潼关断面水深的坝前起始高程Ｚ ，即：
ｗ
＾
Ｚ ＝ Ｋ（ Ｚ － Ｚ ） ＋ Ｚ （１０）
ｗ １ ｄ１ ｄｋ ｃ
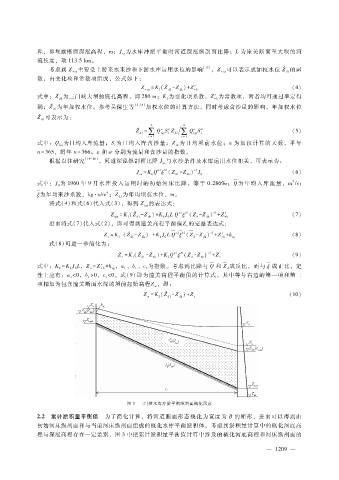
图 ３ 三门峡水库冲淤平衡纵剖面概化示意
２．２ 累计淤积量平衡值 为了简化计算，将河道断面形态概化为宽度为 Ｂ的矩形，进而可以得到由
初始河床纵剖面和与当前河床纵剖面组成的概化水库平衡淤积体。考虑到淤积量计算中的概化河底高
程与深泓高程存在一定差别，图 ３中把累计淤积量平衡值计算中涉及的概化河底高程和河床纵剖面的
— １ ０ ９ —
２