Page 71 - 2022年第53卷第12期

P. 71

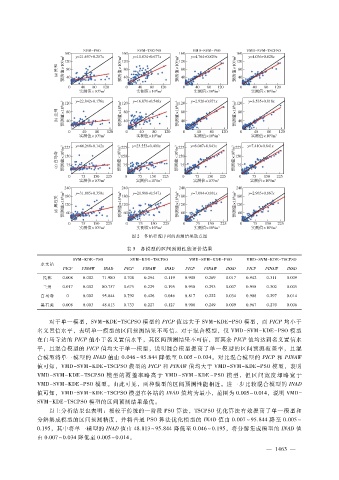
图２各站径流序列的预测结果散点图

表５各模型的区间预测性能评价结果
ＳＶＭ－ＫＤＥ－ＰＳＯＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯＶＭＤ－ＳＶＭ－ＫＤＥ－ＰＳＯＶＭＤ－ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ
水文站
ＰＩＣＰＰＩＮＡＷＩＮＡＤＰＩＣＰＰＩＮＡＷＩＮＡＤＰＩＣＰＰＩＮＡＷＩＮＡＤＰＩＣＰＰＩＮＡＷＩＮＡＤ
民和０．００８０．００２７１．９８００．７０８０．２９４０．１１９０．９０００．２６９０．０１７０．９４２０．３１１０．００９
兰州０．０１７０．００２８０．７５７０．６７５０．２２９０．１９５０．９５００．２９３０．００７０．９５８０．３０２０．００５
白马寺００．００２９５．８４４０．７９２０．４２６０．０４６０．８１７０．２２２０．０３４０．９０８０．２９７０．０１４
黑石关０．００８０．００３４８．８１３０．７３３０．２２７０．１２７０．９０８０．２４９０．００９０．９６７０．２７００．００６

对于单一模型，ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ模型的ＰＩＣＰ值远大于ＳＶＭ－ＫＤＥ－ＰＳＯ模型，而ＰＩＣＰ均小于
名义置信水平，表明单一模型的区间预测结果不可信。对于混合模型，仅ＶＭＤ－ＳＶＭ－ＫＤＥ－ＰＳＯ模型
在白马寺站的ＰＩＣＰ值小于名义置信水平，其区间预测结果不可信，而其余ＰＩＣＰ值均达到名义置信水
平，且混合模型的ＰＩＣＰ值均大于单一模型，说明混合模型提高了单一模型的区间预测覆盖率，且混
合模型将单一模型的ＩＮＡＤ值由０．０４６～９５．８４４降低至０．００５～０．０３４。对比混合模型的ＰＩＣＰ和ＰＩＮＡＷ
值可知，ＶＭＤ－ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ模型的ＰＩＣＰ和ＰＩＮＡＷ值均大于ＶＭＤ－ＳＶＭ－ＫＤＥ－ＰＳＯ模型，表明
ＶＭＤ－ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ模型的覆盖率略高于ＶＭＤ－ＳＶＭ－ＫＤＥ－ＰＳＯ模型，但区间宽度却略宽于
ＶＭＤ－ＳＶＭ－ＫＤＥ－ＰＳＯ模型。由此可见，两种模型的区间预测性能相近。进一步比较混合模型的ＩＮＡＤ
值可知，ＶＭＤ－ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ模型在各站的ＩＮＡＤ值均为最小，范围为０．００５～０．０１４，说明ＶＭＤ－
ＳＶＭ－ＫＤＥ－ＴＳＣＰＳＯ模型的区间预测结果最优。
以上分析结果也表明：相较于传统的一阶段ＰＳＯ算法，ＴＳＣＰＳＯ优化算法有效提高了单一模型和
分解集成模型的区间预测精度，并将普通ＰＳＯ算法优化模型的ＩＮＡＤ值由０．００７～９５．８４４降至０．００５～
０．１９５，其中将单一模型的ＩＮＡＤ值由４８．８１３～９５．８４４降低至０．０４６～０．１９５，将分解集成模型的ＩＮＡＤ值
由０．００７～０．０３４降低至０．００５～０．０１４。

４
— １６３ —

66 67 68 69 70 71 72 73 74 75 76