Page 72 - 2022年第53卷第12期

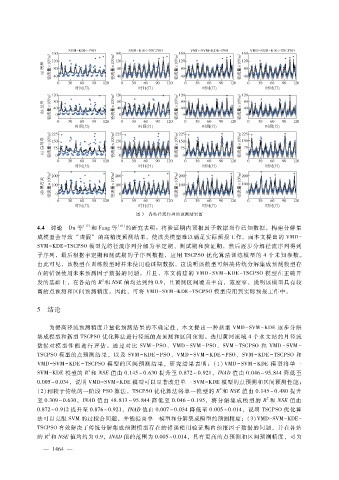
图 ３ 各站径流序列的预测结果图

４．４ 讨论 Ｄｕ等 ［１７］ 和 Ｆａｎｇ等 ［１８］ 的研究表明：将验证期内预报因子数据当作已知数据，构建分解集
成模型会导致 “虚假” 的高精度预测结果，使该类模型难以满足实际预报工作。而本文提出的 ＶＭＤ －
ＳＶＭ－ ＫＤＥ － ＴＳＣＰＳＯ模型先将径流序列分解为率定期、测试期和验证期，然后逐步分解径流序列得到
子序列，最后根据率定期和测试期的子序列数据，应用 ＴＳＣＰＳＯ优化算法训练模型的 ４个未知参数。
由此可见，该模型在训练模型时并未使用验证期数据，这说明该模型可解决传统分解集成预测模型存
在的错误使用未来预测因子数据的问题。并且，本文构建的 ＶＭＤ － ＳＶＭ－ ＫＤＥ － ＴＳＣＰＳＯ模型在正确开
２
发的基础上，在各站的 Ｒ和 ＮＳＥ值均达到约 ０．９，且预测区间覆盖率高，宽度窄，说明该模型具有较
高的点预测和区间预测精度。因此，可将 ＶＭＤ － ＳＶＭ－ ＫＤＥ － ＴＳＣＰＳＯ模型应用到实际预报工作中。

５ 结论

为提高径流预测精度并量化预测结果的不确定性，本文提出一种新型 ＶＭＤ － ＳＶＭ－ ＫＤＥ逐步分解
集成模型和新型 ＴＳＣＰＳＯ优化算法进行径流的点预测和区间预测。选用黄河流域 ４个水文站的月径流
数据对模 型 性 能 进 行 评 估。通 过 对 比 ＳＶＭ－ ＰＳＯ、ＶＭＤ － ＳＶＭ－ ＰＳＯ、ＳＶＭ－ ＴＳＣＰＳＯ和 ＶＭＤ－ ＳＶＭ－
ＴＳＣＰＳＯ模型的点预测 结果，以及 ＳＶＭ－ ＫＤＥ － ＰＳＯ、ＶＭＤ － ＳＶＭ－ ＫＤＥ － ＰＳＯ、ＳＶＭ－ ＫＤＥ － ＴＳＣＰＳＯ和
ＶＭＤ － ＳＶＭ－ ＫＤＥ － ＴＳＣＰＳＯ模型的区间预测结果，研究结果表明：（１）ＶＭＤ － ＳＶＭ－ ＫＤＥ模 型 将单一
２
ＳＶＭ－ ＫＤＥ模型的 Ｒ和 ＮＳＥ值由 ０．１４５～０．６３０提升至 ０．８７２～０．９２１，ＩＮＡＤ值由 ０．０４６～９５．８４４降低至
０．００５～０．０３４，说明 ＶＭＤ － ＳＶＭ－ ＫＤＥ模型可以显著改进单一 ＳＶＭ－ ＫＤＥ模型的点预测和区间预测性能；
２
（ ２）相较于传统的一阶段 ＰＳＯ算法，ＴＳＣＰＳＯ优化算法将单一模型的 Ｒ和 ＮＳＥ值由 ０．１４５～０．４８０提升
２
至 ０．３０９～０．６３０，ＩＮＡＤ值由 ４８．８１３～９５．８４４降低至 ０．０４６～０．１９５，将分解集成模型的 Ｒ 和 ＮＳＥ值由
０．８７２～０．９１２提升至 ０．８７６～０．９２１，ＩＮＡＤ值由 ０．００７～０．０３４降低至 ０．００５～０．０１４，说明 ＴＳＣＰＳＯ优化算
法可以克服 ＳＶＭ的过拟合问题，并能提高单一模型和分解集成模型的预测精度；（３）ＶＭＤ － ＳＶＭ－ ＫＤＥ －
ＴＳＣＰＳＯ有效解决了传统分解集成预测模型存在的错误使用验证期内预报因子数据的问题，并在各站
２
的 Ｒ和 ＮＳＥ值均约为 ０．９，ＩＮＡＤ值的范围为 ０．００５～０．０１４，具有更高的点预测和区间预测精度，可为
— １ ４ ４ —
６