Page 110 - 2023年第54卷第5期

低于无阻尼条件下（真空状态）的固有频率，文
很显然，由于阻尼的存在，实际自由振动的频率 ω ｆ
献［ ２１ － ２２］实际测量的水中自由振动频率低于空气中自由振动频率即说明了这一点。但需要说明的是，
大家约定俗成的称水中设备的自由振动频率为 “水中固有频率”，空气中设备的自由振动频率为 “空
气中固有频率”，其实都不是真正的，而是该阻尼系数下的实际自由振动频率。从严格意义上讲，固
是有阻尼
有频率只有一个，是 ω ０ ，而不是 ω ｆ 。ω ０ 是无阻尼共振或自由振动频率，和阻尼系数无关；ω ｆ
条件下的自由振动频率，和阻尼系数和固有频率均有关。
２．２ 一自由度强迫振动方程的稳态无量纲解 如假定强迫振动为简谐振动，其振动力为 Ｆ·ｓｉｎ（ ω ·ｔ），
线性一自由度强迫振动的运动方程为：
２
ｄｘ ｄｘ
Ｍ ＋ Ｒ ｍ ＋ Ｋ·ｘ ＝ Ｆ·ｓｉｎ（ ω ·ｔ） （５）
２
ｄｔ ｄｔ
Ｋ Ｒ Ｆ
２ ｍ
令ω ０ ＝ ，２ β ＝ ，ｈ ＝ ，则上式变为：
Ｍ Ｍ Ｍ
２
ｄｘ ｄｘ
２
＋ ２ β ＋ ω ０ ·ｘ ＝ ｈ·ｓｉｎ（ ω ·ｔ） （６）
２
ｄｔ ｄｔ
根据微分方程理论，该线性方程的稳态振动解为：
ｘ ＝ Ａ·ｓｉｎ（ ω ·ｔ － φ ） （７）
其振动幅值 Ａ为：
ｈ
Ａ ＝ （８）
２ ２ ２ ２ ２
－
槡 （ ω ０ ω）＋ ４ β ·ω
式中 φ为强迫振动和振动系统之间的相位差，即振动系统与强迫振动之间的滞后角。
为建立无量纲的振动幅值方程，先对式（ ７）（８）的 ３种临界状态进行讨论，以了解其物理意义：
２
０
（ １） ω ＝ ０ 时激振幅值临界状态。如令激振频率 ω ＝ ０ 时的振动幅值为 Ａ，则 Ａ ＝ ｈ? ω ０ ＝ Ｆ?Ｋ。由式
０
（ ５）及刚度系数定义可知，Ｋ为单位位移所需要的弹性力，则强迫振动力 Ｆ与 Ｋ的比 Ａ即该力 Ｆ作用
０
下的原始振动幅值，也就是在静力 Ｆ作用下振动系统的静位移。
时的阻尼系数称为临界阻尼
（ ２） β ＝ ω ０ 时阻尼系数临界状态。通常将 β 等于振动系统固有频率 ω ０
２
２
＋
系数，此时式（ ８）中分母变为 ω ０ ω ，振幅 Ａ的最 大值 出现 在 ω＝ ０时，Ａ ＝ Ａ，其 余 任 何频率下振
０
动幅值都小 于 激 振 幅 值， 说 明 没 有 共 振 发 生。 这 说 明， 所 谓 的 临 界 阻 尼 系 数 是 指 共 振 发 生 的 门
槛值。
时激振频率临界状态———速度共振状态。在该振动频率，振动速度达到最大值。在有阻
（ ３） ω ＝ ω ０
尼的条件下，位移振动最大值并没有出现在该点。当阻尼比较小时，移振动最大值靠近该频率。
因此，可分别用振动幅值 Ａ、阻尼系数 β 、振动频率 ω和各自的临界值之比进行无量纲化，并令
，则式（８）变为：
０
振动幅值比 ａ ＝ Ａ?Ａ，阻尼比 ξ ＝ β ? ω ０ ，振动频率比 ｗ ＝ ω ? ω ０
１
ａ ＝ （９）
２ ２ ２ ２
槡 （１ － ｗ）＋ ４ ξ ·ｗ
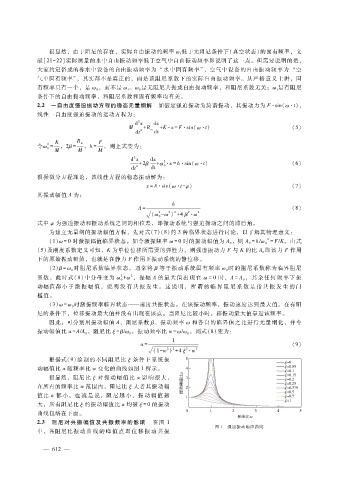
根据式（９）绘制的不同阻尼比 ξ 条件下系统振
动幅值比 ａ随频率比 ｗ变化的曲线如图 １所示。
很显然，阻尼比 ξ 对振动幅值比 ａ影响很大，
在所有的频率比 ｗ范围内，阻尼比 ξ 大者其振动幅
值比 ａ都 小。也 就 是 说，阻 尼 越 小，振 动 幅 值 越
大，所有阻尼比 ξ 的振动幅值比 ａ均被 ξ ＝ ０的振动
曲线包络在下面。
２．３ 阻尼对共振幅值及共振频率的影响 在 图 １
图 １ 强迫振动响应曲线
中，各阻尼比振 动 曲 线 的 峰 值 点 即 位 移 振 动 共 振

２
— ６ １ —