Page 111 - 2023年第54卷第5期

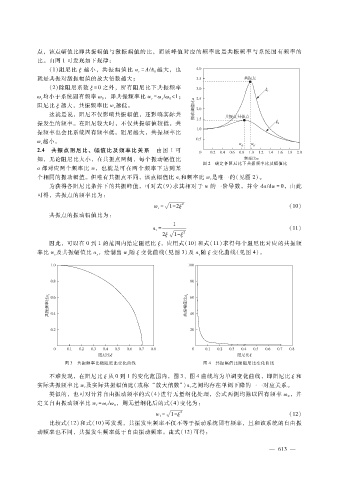
点，该点幅值比即共振幅值与激振幅值的比，而该峰值对应的频率比是共振频率与系统固有频率的
比。由图 １可发现如下规律：
（１）阻尼比 ξ 越小，共振幅值比 ａ＝ Ａ?Ａ越大，也
０
ｒ
就是共振对激振幅值的放大倍数越大；
（ ２）除阻尼系数 ξ ＝ ０ 之外，所有阻尼比下共振频率
? ＜１；
ω ｒ 均小于系统固有频率 ω ０ ，即共振频率比 ｗ＝ ω ｒ ω ０
ｒ
阻尼比 ξ 越大，共振频率比 ｗ越低。
ｒ
这就是说，阻尼不仅影响共振幅值，还影响实际共
振发生的频率。在阻尼较大时，不仅共振幅值较低，共
振频率也会比系统固有频率低。阻尼越大，共振频率比
ｗ越小。
ｒ
２．４ 共振点阻尼比、幅值比及频率比关系 由图 １可
知，无论阻尼比大小，在共振点两侧，每个振动幅值比
图 ２ 确定各阻尼比下共振频率比及幅值比
ａ都对应两个频率比 ｗ，也就是可在两个频率下达到某
个相同的振动幅值。但唯有共振点不同，该点幅值比 ａ和频率比 ｗ是唯一的（见图 ２）。
ｒ ｒ
为获得各阻尼比条件下的共振峰值，可对式（９）求其相对于 ｗ的一阶导数，并令 ｄａ?ｄｗ ＝ ０，由此
可得，共振点的频率比为：

２
ｗ＝ １ － ２ ξ （１０）
ｒ 槡
共振点的振动幅值比为：
１
ａ＝ （１１）
ｒ
２
２ ξ １ － ξ
槡
因此，可以在 ０到 １的范围内给定阻尼比 ξ ，应用式（１０）和式（１１）求得每个阻尼比对应的共振频
率比 ｗ及共振幅值比 ａ，绘制出 ｗ随 ξ 变化曲线（见图 ３）及 ａ随 ξ 变化曲线（见图 ４）。
ｒ ｒ ｒ ｒ

图 ３ 共振频率比随阻尼比变化曲线 图 ４ 共振幅值比随阻尼比变化曲线

不难发现，在阻尼比 ξ 从 ０到 １的变化范围内，图 ３、图 ４曲线均为单调变化曲线，即阻尼比 ξ 和
实际共振频率比 ｗ及实际共振幅值比（或称 “放大倍数”）ａ之间均存在单调下降的一一对应关系。
ｒ ｒ
，并
类似的，也可对计算自由振动频率的式（４）进行无量纲化处理，公式两侧均除以固有频率 ω ０
? ，则无量纲化后的式（４）变化为：
ｆ
定义自由振动频率比 ｗ＝ ω ｆ ω ０
２
ｗ＝ １ － ξ （１２）
ｆ 槡
比较式（ １２）和式（１０）可发现，共振发生频率不仅不等于振动系统固有频率，且和该系统的自由振
动频率也不同，共振发生频率低于自由振动频率。由式（１２）可得：

— ６ １ ３ —