Page 41 - 2024年第55卷第7期

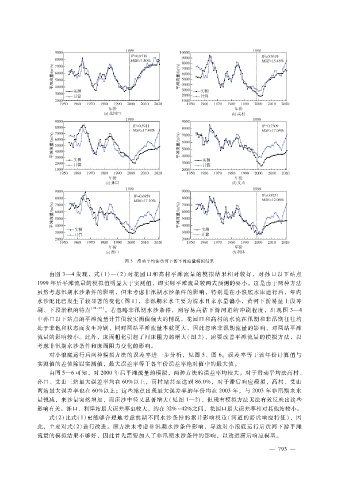
图 ３ 滑动平均法黄河下游平滩流量模拟结果

由图 ３—４发现，式（１）—（２）对花园口和高村平滩流量的模拟结果相对较好，对孙口以下站点
１９９９年后平滩流量的模拟值明显大于实测值，即实际平滩流量较两式预测的要小。这是由于两种方法
虽然考虑汛期水沙条件的影响，但未考虑非汛期水沙条件的影响，特别是在小浪底水库运行后，年内
水沙配比已发生了较显著的变化（图 １），非汛期来水主要为清水且来水量偏小，黄河下游易呈上段冲
刷、下段淤积的特点 ［３１ － ３３］ 。若忽略非汛期水沙条件，则容易高估下游河道的冲刷程度，出现图 ３—４
中孙口以下站点的平滩流量计算值较实测值偏大的情况。花园口和高村的水流在汛期和非汛期往往均
处于非饱和状态而发生冲刷，同时两站平滩流量本就更大，因此忽略非汛期流量的影响，对两站平滩
流量的影响较小。此外，床面粗化引起了河床阻力的增大（图 ２），需要改善平滩流量的模拟方法，以
考虑非汛期水沙条件和床面阻力变化的影响。
对小浪底运行后两种模拟方法的误差率进一步分析，见图 ５、图 ６。误差率等于该年份计算值与
实测值的差值除以实测值，最大误差率等于各年份误差率绝对值中的最大值。
由图 ５—６可知，对 ２０００年后平滩流量的模拟，两种方法的误差率均较大。对于滑动平均法高村、
孙口、艾山三站最大误差率均在 ６０％以上，高村站甚至达到 ８６．０％，对于滞后响应模拟，高村、艾山
两站最大误差率也在 ６０％以上；这些站点出现最大误差率的年份均在 ２００３年，与 ２００３年非汛期来水
量锐减，来沙量突然增加，而床沙中径又显著增大（见图 １—２），但现有模拟方法无法有效反映出这些
影响有关。泺口、利津站最大误差率也较大，约在 ３２％～４２％之间，花园口最大误差率相对其他站较小。
式（２）比式（１）更能够合理地考虑前期不同水沙条件的累计影响权重（河道的滞后响应特征），因
此，主要对式（ ２）进行改进。原方法未考虑非汛期水沙条件影响，导致对小浪底运行后黄河下游平滩
流量的模拟结果不够好，因此首先需要加入了非汛期水沙条件的影响，以改进滞后响应模型。

— ７ ９ ３ —