Page 49 - 2021年第52卷第8期

)
度，f 为单轴抗压强度，一般取 f /f =1.16，故α=0.12； β = C c (1 - α - (1 + α )，C 、C 分别为有效抗
co bo co c t
C t
压强度和有效抗拉强度。
为把单轴试验的损伤演化规律应用于多维体系的应力状态中，目前大多采取以多维体系中的最
大和最小主应变ε max 和ε min 替代单轴受拉和受压试验中的ε t 和ε c ，但由于混凝土的拉压损伤演化规律的
差异，引入了一个考虑复杂应力状态时的拉、压应力间相互影响的加权因子：
σ
r ( ) = ∑ σ ∑ || σ ， 0 < r < 1 （8）
i i
式中： σ 为多维应力状态的主应力；〈x〉为 Macaulay括弧函数，当 x为正值时取 x值，当 x为负值时取为零。
由于混凝土抗压强度远高于抗拉强度，在暂不考虑受压损伤时，最终在多维体系中采用的等效
弹性模量为：
͂
E = (1 - rd t )E 0 （9）
p
当卸载至拉应力趋于零时，ε max 接近ε ，在多维体系中用等效弹性模量求得的应变张量ε ij 即为初
p
p
p
始卸载应力相应的残余应变张量ε ij ，其相应的变形张量为u ij 。ε max 小于ε 时，多维体系转向受压为主
的情况，按等效初始弹性模量对自变量 u-u 求解。考虑残余应变的混凝土损伤模型完全不涉及塑性
p
理论，概念清晰合理，计算也更为简便。
本文在 1500 吨 MTS 大型材料动态性能试验机上进行某大坝全级配混凝土轴拉全过程试验，试验
采用“加卸载非等速率”的控制方式 ［14］ 获得动态的轴拉加卸载循环应力应变全过程曲线如图 2，其中引
伸计数据给出的位移-荷载曲线图形更为稳定完整，故采用引伸计数据转换作为测定的应力应变全过
程曲线试验数据，经统计回归整理得到典型应力－应变全过程曲线，包括应力-应变关系包络线和卸
载、再加载的往复循环曲线的数学表达式。

-6
应变ε×10
0 200 400 600 800 1000 1200
300
应变-荷载曲线
250
位移-荷载曲线
200
荷载/kN 150

100
50
0
-50
0.0 0.1 0.2 0.3 0.4 0.5 0.6
平均位移值/mm

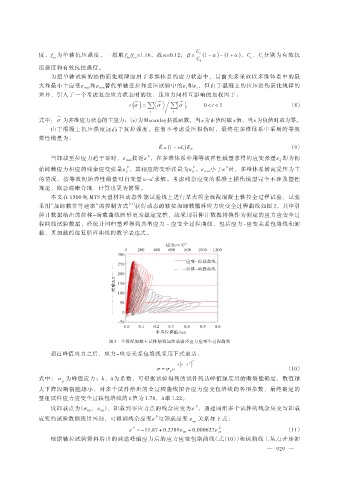
图 2 全级配混凝土试件轴拉加卸载循环应力应变全过程曲线
超过峰值应力之后，应力-应变关系包络线采用下式表达：
-k( ε - ε p ) λ
σ = σ p e （10）
式中： σ 为峰值应力；k、λ为系数，可根据试验得到的试件到达峰值强度后的断裂能确定，数值越
p
大下降段断裂能越小，对多个试件给出的全过程曲线拟合应力应变包络线的各项参数，最终确定的
整组试件应力应变全过程包络线的 k 值为 1.78，λ取 1.22。
p
设卸载点为（σ un ，ε un ），卸载到零应力点的残余应变为ε ，通过同组多个试件的残余应变与卸载
p
应变的试验数据统计回归，可得到残余应变ε 与卸载应变 ε 关系如下式：
un
p 2 （11）
ε = -11.87 + 0.2389ε un + 0.000627ε un
根据轴拉试验资料给出的到达峰值应力后的应力应变包络曲线（式（10））和该曲线上某点开始卸
— 929 —