Page 53 - 2021年第52卷第8期

35
30
25
× 10 -6 20
ε q 15
10
5
0
0 50 100 150 200 250 300 350 400
p
ε × 10 -6
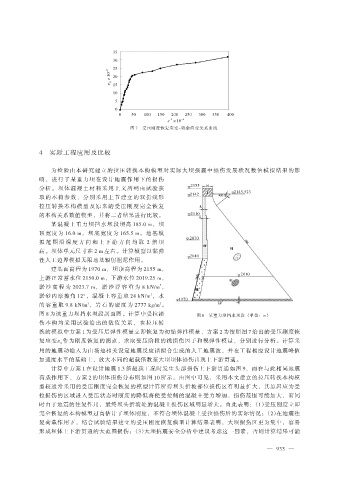
图 7 受压刚度恢复应变-残余应变关系曲线

4 实际工程应用及比较

为检验由本研究建立的拉压转换本构模型对实际大坝强震中损伤发展状况数值模拟结果的影
响，进行了某重力坝在设计地震作用下的损伤
分析。坝体混凝土材料采用上文所列由试验获 2155
2145.523
取的本构参数，分别采用上节建立的双折线形 2142
拉压转换本构模型及原来的受压刚度完全恢复
的本构关系数值模型，并将二者结果进行比较。 2110
某混凝土重力坝挡水坝段坝高 185.0 m，坝
顶宽度为 16.0 m，坝底宽度为 165.5 m。地基模
2070
拟 范 围 沿 深 度 方 向 和 上 下 游 方 向 均 取 2 倍 坝
高。坝体单元尺寸在 2 m 左右。计算模型以黏弹
2040
性人工边界模拟无限地基辐射阻尼作用。
建基面高程为 1970 m，坝顶高程为 2155 m，
2010
上游正常蓄水位 2150.0 m，下游水位 2019.25 m，
淤 沙 高 程 为 2023.7 m， 淤 沙 浮 容 重 为 8 kN/m ，
3
淤砂内摩擦角 12°，混凝土容重取 24 kN/m ，水
3
1970
的 容 重 取 9.8 kN/m ， 岩 石 的 密 度 为 2777 kg/m 。
3
3
图 8 为该重力坝挡水坝段剖面图。计算中受拉损 图 8 某重力坝挡水坝段 （单位：m）
伤本构均采用试验给出的数值关系，在拉压转
换的模拟中方案 1 为受压后弹性模量立即恢复为初始弹性模量，方案 2 为按照图 7 给出的受压刚度恢
复应变ε q 作为刚度恢复的拐点，求取受压阶段的视损伤因子和视弹性模量，分别进行分析。计算采
用的地震动输入为由场地相关设定地震反应谱拟合生成的人工地震波，并在工程相应设计地震峰值
加速度水平的基础上，放大不同的超载倍数至大坝坝体损伤出现上下游贯通。
计算中方案 1 在设计地震 1.3 倍超载工况时发生头部损伤上下游贯通如图 9，而在与此相同地震
荷载作用下，方案 2 的坝体损伤分布则如图 10 所示。由图中可见，采用本文建立的拉压转换本构模
型较通常采用的受压刚度完全恢复的模型计算所得坝头折坡部位损伤区有明显扩大，其原因应为受
拉损伤的区域进入受压状态时刚度的降低将使受拉侧的混凝土受力增加，损伤范围可能加大，而同
时由于地震的往复作用，最终坝头折坡处的混凝土损伤区域明显增大。由此表明：（1）受压刚度立即
完全恢复的本构模型过高估计了坝体刚度，不符合坝体混凝土受拉损伤后的实际情况；（2）在地震往
复荷载作用下，结合试验结果建立的受压刚度恢复模型计算结果表明，大坝损伤区更为集中，容易
形成坝体上下游贯通的大范围损伤；（3）大坝抗震安全分析中建议考虑这一因素，否则计算结果可能

— 933 —