Page 50 - 2021年第52卷第8期

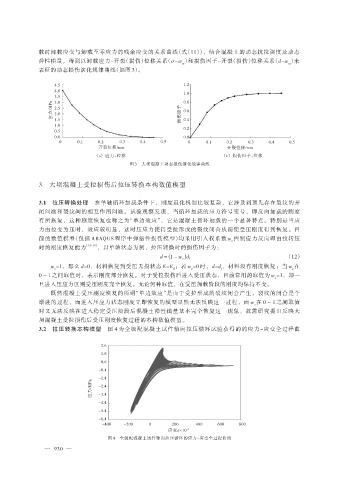
载时卸载应变与卸载至零应力的残余应变的关系曲线（式（11）），结合混凝土的动态抗拉强度及动态
弹性模量，得到以卸载应力-开裂（损伤）位移关系（σ-w ）和损伤因子-开裂（损伤）位移关系（d-w ）来
cr cr
表征的动态损伤演化规律曲线（如图 3）。

4.5 1.2
4.0
1.0
3.5 0.8
应力/MPa 2.5 损伤因子 0.6
3.0
2.0
1.5 0.4
1.0
0.2
0.5
0.0 0.0
0 0.1 0.2 0.3 0.4 0.5 0 0.1 0.2 0.3 0.4 0.5
开裂位移/mm 开裂位移/mm
（a） 应力-位移 （b） 损伤因子-位移
图 3 大坝混凝土动态损伤演化规律曲线

3 大坝混凝土受拉损伤后拉压转换本构数值模型

3.1 拉压转换处理 在单轴循环加载条件下，刚度退化机制比较复杂，它涉及到预先存在裂纹的开
闭问题和裂纹间的相互作用问题。试验观察发现，当循环加载的应力符号变号，即反向加载的刚度
有所恢复，这种刚度恢复也称之为“单边效应”，它是混凝土循环加载的一个显著特点。特别是当应
力由拉变为压时，效应较明显，这时压应力使得受拉形成的裂纹闭合从而使受压刚度得到恢复。目
前的数值模型（包括 ABAQUS 程序中弹塑性损伤模型）均采用引入权系数 w 控制应力反向即由拉转压
c
时的刚度恢复能力 ［15-18］ ，以单轴状态为例，拉压转换时的损伤因子为：
（12）
d = (1 - w c )d t
w =1，那么 d=0，材料恢复到受压无损状态 E=E ；若 w =0 时，d=d ，材料没有刚度恢复；当 w 在
c 0 c t c
0 ~ 1 之间取值时，表示刚度部分恢复。对于受拉损伤后进入受压状态，目前常用的取值为 w =1，即一
c
旦进入压应力区则受压刚度完全恢复。无论何种取值，在受压加载阶段的刚度均保持不变。
既然混凝土受压刚度恢复的所谓“单边效应”是由于受拉形成的裂纹闭合产生，裂纹的闭合是个
渐进的过程，而进入压应力状态刚度立即恢复的模型显然无法反映这一过程，而 w 在 0 ~ 1 之间取值
c
时又无法反映在进入稳定受压阶段后混凝土弹性模量基本完全恢复这一现象，故需研究提出反映大
坝混凝土受拉损伤后受压刚度恢复过程的本构数值模型。
3.2 拉压转换本构模型 图 4 为全级配混凝土试件轴向拉压循环试验获得的的应力-应变全过程曲

2.6
1.6
0.6
-0.4
-1.4
应力/MPa -2.4
-3.4
-4.4
-5.4
-6.4
-400 -200 0 200 400 600 800
-6
应变ε×10
图 4 全级配混凝土试件轴向拉压循环的应力-应变全过程曲线
— 930 —