Page 51 - 2021年第52卷第8期

线。由图 4 可见，在发生受拉损伤后，即拉应力峰值过后进行卸载并到达压应力区时 ，受压弹性模
量并非立即恢复，也不是保持某一数值不变，而是以渐进的形式，随着压应力的增加，逐渐由受拉
损伤后的弹性模量恢复至初始弹性模量。显然，受压弹性模量固定不变的假定与试验给出的实际情
况不符，尤其是认为受压弹性模量立即完全恢复的简化方式，有可能过高估计混凝土材料进入受压
区后的刚度，而偏于不安全。
为建立拉压转换本构关系的数值模型，既需考虑混凝土材料受拉损伤后进入受压状态时弹性模
量逐渐恢复的过程，又需考虑计算分析中数值模型的简易可行，因为考虑材料动态损伤后的本构关
系数值模拟已相当复杂，再采用过于繁琐的拉压转换模拟会给计算分析带来较大困难及计算耗时的
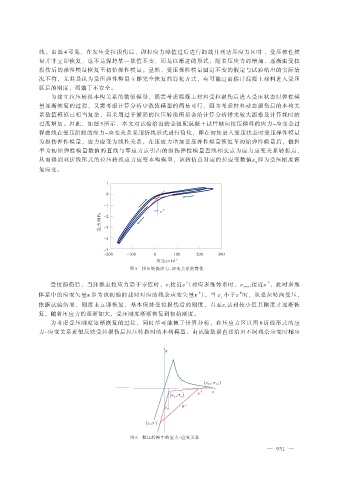
过度增加。因此，如图 5 所示，本文对试验给出的全级配混凝土试件轴向拉压循环的应力-应变全过
程曲线在受压阶段的应力-应变关系采用折线形式进行简化，即在初始进入受压状态时受压弹性模量
为损伤弹性模量，应力应变为线性关系，在压应力增加受压弹性模量恢复至初始弹性模量后，做斜
率为初始弹性模量数值的直线与零应力点引出的损伤弹性模量直线相交点为应力应变关系转折点，
从而得到双折线形式的拉压转换应力应变本构模型，该转折点对应的拉应变数值ε q 即为受压刚度恢
复应变。

1
0

-1
ε p
应力/MPa -3
-2

-4
-5
-200 -100 0 100 200 300
-6
应变ε×10
图 5 拉压转换应力-应变关系的简化

p
p
受拉损伤后，当卸载至拉应力趋于零值时，ε t 接近ε （对应多维体系时，ε max t 接近ε ，此时多维
p
p
体系中的应变矢量ε 即为该初始卸载时对应的残余应变矢量ε ）。当 ε 小于ε 时，从受拉转向受压，
t
依据试验结果，刚度未立即恢复，基本保持受拉损伤后的刚度，直至ε t 达到较小值其刚度才逐渐恢
复，随着压应力的逐渐加大，受压刚度渐渐恢复到初始刚度。
为考虑受压刚度逐渐恢复的过程，同时尽可能便于计算分析，在压应力区以图 6 折线形式的应
力-应变关系近似反映受拉损伤后拉压转换时的本构模型。由试验数据直接给出不同残余应变时相应

σ

)
(ε un ,σ un
) ε p ε
(ε q ,σ q
-
E ′
ε q
(ε,σ )

图 6 拉压转换中的应力-应变关系
— 931 —