Page 47 - 2022年第53卷第10期

４．２ 水文干旱历时－ 烈度联合分布模型的构建 华县、张家山、状头站水文干旱历时、烈度均在 ９５％
的置信度下通过了 Ｐｅａｒｓｏｎ相关检验，具有显著相关性。选用水文领域三种应用广泛的 Ａｒｃｈｉｍｅｄｅａｎ型
Ｃｏｐｕｌａ函数（ＣｌａｙｔｏｎＣｏｐｕｌａ、ＦｒａｎｋＣｏｐｕｌａ、ＧｕｍｂｅｌＣｏｐｕｌａ）构建渭河流域水文干旱历时－ 烈度的联合分
布模型，利用 Ｇｒｉｎｇｏｒｔｅｎ经验频率公式计算历时、烈度的边缘分布，以极大似然法估计 Ｃｏｐｕｌａ函数的
参数，结果如表 ２所示 ［３７ － ３８］ 。基于 ＡＩＣ准则 ［３７］ 选择最优的 Ｃｏｐｕｌａ函数，华县、张家山、状头站分别
为 ＣｌａｙｔｏｎＣｏｐｕｌａ、ＦｒａｎｋＣｏｐｕｌａ、ＧｕｍｂｅｌＣｏｐｕｌａ。

表 ２ 干旱历时、烈度联合分布模型参数
Ｃｏｐｕｌａ函数
水文站 参数
Ｃｌａｙｔｏｎ Ｆｒａｎｋ Ｇｕｍｂｅｌ
θ ７．３５ １） １７．２０ ４．６９
华县
ＡＩＣ值 － １２４ ．３０ １） － １０５．６９ － １１２．７６
θ ５．４８ １７．１６ １） ４．０６
张家山
ＡＩＣ值 － １０１．４５ － １０６．３２ １） － ９９．３１
θ ４．６１ １４．５７ ３．７５ １）
状头
ＡＩＣ值 － ８８．１２ － ９０．６７ － ９１．４１ １）
注：１）代表最优 Ｃｏｐｕｌａ函数的参数。

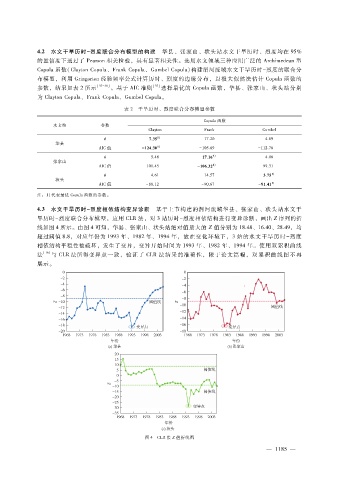
４．３ 水文干旱历时－ 烈度相依结构变异诊断 基于上节构建的渭河流域华县、张家山、状头站水文干
旱历时－ 烈度联合分布模型，应用 ＣＬＲ法，对 ３站历时－ 烈度相依结构进行变异诊断，画出 Ｚ序列的折
线如图 ４所示。由图 ４可知，华县、张家山、状头站绝对值最大的 Ｚ值分别为 １８．４８、１６．４０、２８．４９，均
超过阈值 ８．８，对应年份为 １９９３年、１９８２年、１９９４年，故在变化环境下，３站的水文干旱历时 － 烈度
相依结构平稳性被破坏，发生了变异，变异开始时间为 １９９３年、１９８２年、１９９４年。使用双累积曲线
法 ［１６］ 与 ＣＬＲ法所得变异点一致，验证了 ＣＬＲ法结果的准确性，限于论文篇幅，双累积曲线图不再
展示。

图 ４ ＣＬＲ法 Ｚ值折线图
１
— １ ８ ５ —