Page 56 - 2023年第54卷第6期

－ ４
３
由表 ２可知，式（１）的平均相对误差（ＡＲＥ）为 １．９３％，均方根误差（ＲＭＳＥ）为 ２．００ × １０ ｍ ?ｓ，标
准误差（ ＳＥ）为 ２．０３％，标准均方根误差（ＮＲＭＳＥ）为 ０．８８％，说明式（１）的计算精度较高。
用式（ １）计算各试验工况的实测值和计算值的相对误差的绝对值 δ （ δ ＝ Ｑ － Ｑ ?Ｑ ），并将其点绘
０
Ｃ
０
在图 ８中。从图中可以看出，相对误差小于 ６％的占比为 ９６．２％，小于 ４％占比为 ８９．５％。

图 ８ 相对误差的绝对值

为了检验式（１）的计算精度，选取表 １中未参与公式推导的 ５４组试验数据进行验证。结果表明，
式（ １）的相对误差小于 ６％的数据占比为 ９６．３％，小于 ４％的数据占比 ８８．９％。还选用平均相对误差
（ ＡＲＥ）、均方根误差（ＲＭＳＥ）、标准误差（ＳＥ）和标准均方根误差（ＮＲＭＳＥ）对式（１）的计算精度进行评
价，具体结果见表 ３。由表 ３可知用式（１）平均相对误差（ＡＲＥ）为 ２．１７％，均方根误差（ＲＭＳＥ）为 ２．８０ ×
３
－ ４
１０ ｍ ?ｓ，标准误差（ＳＥ）为 ２．５０％，标准均方根误差（ＮＲＭＳＥ）为 １．２０％。
表 ３ 验证数据的各评价指标计算结果
３
ＡＲＥ?％ ＲＭＳＥ?（ｍ ?ｓ） ＳＥ?％ ＮＲＭＳＥ?％
２．１７ ２．８０ × １０ － ４ ２．５０ １．２０

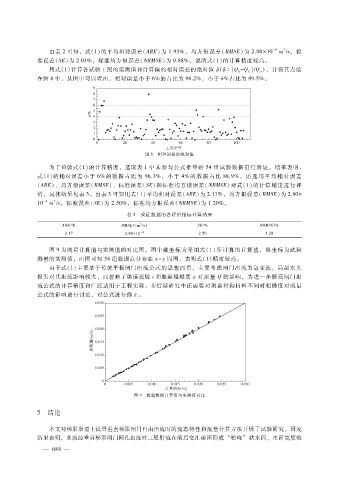
图 ９为流量计算值与实测值的对比图，图中横坐标为采用式（１）所计算的计算值，纵坐标为试验
测量的实测值，由图可知 ５４组数据点分布在 ｘ ＝ ｙ周围，表明式（１）精度较高。
由于式（１）主要基于传统平板闸门出流公式的思想而得，主要考虑闸门出流为急变流，局部水头
损失对其出流影响较大，而忽略了渠道底坡 ｉ和渠道粗糙度 ε对流量 Ｑ的影响，为进一步提高闸门出
流公式的计算精度和广泛适用于工程实际，在后续研究中还需要对渠道衬砌材料不同时粗糙度对流量
公式的影响进行讨论，对公式进行修正。

图 ９ 检验数据计算值与实测值对比

５ 结论

本文对梯形渠道上设置垂直梯形闸门自由出流时的流态特性和流量计算方法开展了试验研究。研究
结果表明，水流经垂直梯形闸门闸孔出流时三股射流在闸后交汇碰撞形成 “驼峰” 状水面，水面宽度收
— ６ ８ —
４