Page 125 - 2024年第55卷第1期

式中：ｎ为沿着裂缝面的切向单位向量；ｎ为裂缝面法向单位向量；ｋ为弹簧刚度系数； 珘
Ａ为弹簧节点
ｓ ｎ
的控制面积。

５ 数值算例

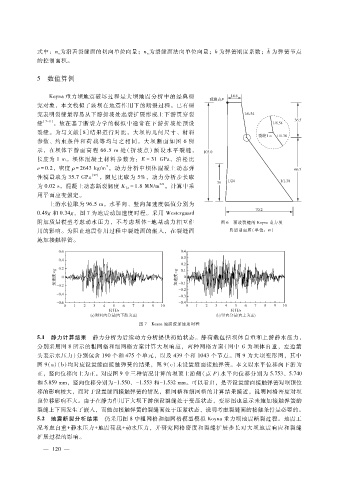
Ｋｏｙｎａ重力坝地震破坏过程是大坝地震分析中的经典研
究对象，本文模拟了该坝在地震作用下的断裂过程。已有研
究表明裂缝最容易从下游折坡处起裂扩展形成上下游贯穿裂
缝 ［７ － ８］ ，故在基于断裂力学的模拟中通常在下游折坡处预设
裂缝。为与文献［ ８］结果进行对比，大坝的几何尺寸、材料
参数、约束条 件 和 荷 载 等 均 与 之 相 同。大 坝 断 面 如 图 ６所
示，在坝体下 游面 高 程 ６６．５ｍ处 （折坡 点）预 设 水 平 裂 缝，
长度为 １ｍ。坝体混凝土材 料参数 为：Ｅ＝ ３１ＧＰａ ，泊松 比
３
ν ＝ ０．２，密度 ρ ＝ ２６４３ｋｇ?ｍ 。动力分析中坝体混凝土动态弹
［２７］
性模量取为 ３５．７ＧＰａ ，阻尼比取为 ５％，动力分析步长取
３?２
为 ０．０２ｓ，混凝土动态断裂韧度 Ｋ ＝ １．８ＭＮ?ｍ 。计算中采
Ⅰ ｄ
用平面应变假定。
上游水位取为 ９６．５ｍ。水平向、竖向加速度幅值分别为
０．４９ｇ和 ０．３４ｇ，图 ７为地震动加速度时程。采用 Ｗｅｓｔｅｒｇａａｒｄ
附加质量模型考虑动水压力，不考虑坝体 － 地基动力相互作 图 ６ 预设裂缝的 Ｋｏｙｎａ重力坝
用的影响。为阻止地震作用过程中裂缝面的嵌入，在裂缝面 典型剖面图（单位：ｍ）
施加接触弹簧。

图 ７ Ｋｏｙｎａ地震波加速度时程

５．１ 静力计算结果 静力分析为后续动力分析提供初始状态。静荷载包括坝体自重和上游静水压力，
分别采用图 ８所示的粗网格和细网格方案计算大坝响应，两种网格方案（图中 Ｇ为坝体自重，左边箭
头表示水压力）分别包含 １９０个和 ４７５个单元，以及 ４３９个和 １０４３个节点。图 ９为大坝变形图，其中
图 ９（ａ）（ｂ）均对应设置缝面接触弹簧的结果，图 ９（ｃ）未设置缝面接触弹簧。本文以水平位移向下游为
正，竖向位移向上为正。对应图 ９中三种情况计算的坝顶上游侧（点 Ｐ）水平向位移分别为 ５．７５３、５．７４０
和 ５．８５９ｍｍ，竖向位移分别为－ １．５５０ 、－ １．５５３ 和－ １．５３２ｍｍ 。可以看出，是否设置缝面接触弹簧对坝顶位
移的影响较大，而对于设置缝面接触弹簧的情况，粗网格和细网格的计算结果接近，说明网格密度对坝
顶位移影响不大。由于在静力作用下大坝下游预设裂缝处于受压状态，变形图也显示未施加接触弹簧的
裂缝上下面发生了嵌入，而施加接触弹簧的裂缝面处于压紧状态，说明考虑裂缝面的接触条件是必要的。
５．２ 地震断裂分析结果 仍采用图 ８中粗网格和细网格模型模拟 Ｋｏｙｎａ重力坝地震断裂过程。地震工
况考虑自重＋ 静水压力＋ 地震荷载＋ 动水压力，并研究网格密度和裂缝扩展步长对大坝地震响应和裂缝
扩展过程的影响。

０
— １ ２ —