Page 47 - 2024年第55卷第1期

Ｙａｌｉｎ式：
槡 [
１
Φ＝ ０ ．６３５Ｒ Θ １ － ｌｎ（１ ＋ ａＲ） ] （１５）
ａＲ
［３０］
式中：目前公认 Θ ｃ ＝ ０．０２７５Ｆｒ ，Ｆｒ为弗劳德数，式（１１）（１２）中取 Θ ｃ ＝ ０．０４７，式 （１３）中取 Θ ｃ ＝
３?２
[ 槡 ρ Ｕ １?６] １?４
＝ ０．０１６ ；Θ ′为无因次形式的沙粒剪切力，Θ ′ ＝ （ γ ｈＪ） ；式
０．０２９ ，式（１４）中取 Θ ｃ
７．６８（ｈ?ｄ ）
５０
γ
槡 ( ) ２?５ ，Ｒ ＝ Θ － Θ ｃ

（ １５）中 Θ ｃ 为查希尔兹曲线，ａ ＝ ２．４５ Θ ｃ 。
γ ｓ Θ ｃ
Ｅｉｎｓｔｅｉｎ式：
－
γ ｓ γｄ ３５
ψ ＝ （１６）
γ Ｒ′Ｊ
ｂ
Ｂ  ψ － １? η ０
１ － ｔ ２ Ａ Φ

１－ ∫ ｅ ｄｔ ＝ （１７）
１＋Ａ Φ
槡 π－ Ｂ  ψ － １? η ０ 
根据试验资料可分别取 １?０．０２３、１?７和 ０．５。
ｂ
式中：Ｒ′为沙粒阻力对应的水力半径，ｍ；Ａ 、Ｂ 和 η ０


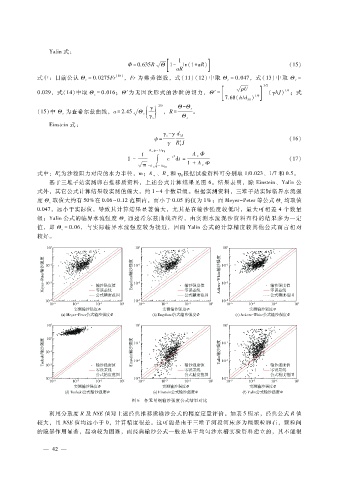
基于三堆子站实测卵石推移质资料，上述公式计算结果见图 ６。结果表明，除 Ｅｉｎｓｔｅｉｎ、Ｙａｌｉｎ公
式外，其它公式计算结果较实测值偏大，约 １～４个数量级。根据实测资料，三堆子站实际临界水流强
均取值
度 Θ ｃ 取值大约有 ５０％在 ０．０６～０．１２范围内，而小于 ０．０５的仅为 １％；而 Ｍｅｙｅｒ － Ｐｅｔｅｒ等公式 Θ ｃ
０．０４７，远小于实际值，导致其计算结果显著偏大，尤其是在输沙强度较低时，最大可相差 ４个数量
通过希尔兹曲线查得，由实测水流泥沙资料查得的结果多为一定
级；Ｙａｌｉｎ公式的临界水流强度 Θ ｃ
＝ ０．０６ ，与实际临界水流强度较为接近，因而 Ｙａｌｉｎ公式的计算精度较其他公式而言相对
值，即 Θ ｃ
较好。

图 ６ 各无量纲输沙强度公式结果对比

利用分散度 Ｒ及 ＮＳＥ值对上述经典推移质输沙公式的精度定量评价。如表 ５所示，经典公式 Ｒ值
较大，且 ＮＳＥ值均远小于 ０，计算精度很差。这可能是由于三堆子河段河床多为粗颗粒卵石，颗粒间
的隐暴作用显著，起动较为困难，而经典输沙公式一般是基于均匀沙水槽实验资料建立的，其不能很

— ４ ２ —