Page 46 - 2024年第55卷第1期

沙率公式能全面反映卵石河床推移质输沙规律，并与不同河流实测资料吻合较好；且部分此类公式形
式复杂，计算繁琐。本文分别从推移质输沙率关系与单一水流因子的建立、经典无因次推移质输沙公
式结果比较、通用无因次推移质输沙公式建立三个方面，确定出适合三堆子河段的推移质输沙公式。
４．１ 单一水流因子 按照生产部门常用的资料整编方法，将三堆子站卵石推移质输沙率与对应的实测
流量及平均流速建立如下指数形式关系：
Ｇ＝ ｐＱ ｑ （７）
ｓ
Ｇ＝ ｒＶ ｓ （８）
ｓ
３
式中：Ｇ为断面卵石推移质输沙率，ｋｇ?ｓ；Ｑ为流量，ｍ ?ｓ；Ｖ为断面平均流速，ｍ?ｓ；ｐ、ｒ为单一水
ｓ
流因素系数；ｑ、ｓ为指数。
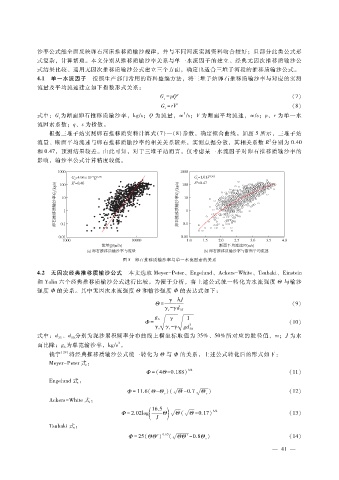
根据三堆子站实测卵石推移质资料计算式（ ７）—（８）参数，确定拟合曲线。如图 ５所示，三堆子站
２
流量、断面平均流速与卵石推移质输沙率的相关关系较差，实测点据分散，其相关系数 Ｒ分别为 ０．４０
和 ０．４７，预测结果较差。由此可知，对于三堆子站而言，仅考虑某一水流因子对卵石推移质输沙率的
影响，输沙率公式计算精度较低。

图 ５ 卵石推移质输沙率与单一水流因素的关系

４．２ 无因次经典推移质输沙公式 本文选取 Ｍｅｙｅｒ － Ｐｅｔｅｒ、Ｅｎｇｅｌｕｎｄ、Ａｃｋｅｒｓ － Ｗｈｉｔｅ、Ｔｓｕｂａｋｉ、Ｅｉｎｓｔｅｉｎ
和 Ｙａｌｉｎ六个经典推移质输沙公式进行比较。为便于分析，将上述公式统一转化为水流强度 Θ与输沙
强度 Φ 的关系。其中无因次水流强度 Θ和输沙强度 Φ 的表达式如下：
γ ｈＪ
Θ＝ （９）
－
γ ｓ γ ｄ ３５
ｇ ｂ γ １
Φ＝ （１０）
槡 槡
－
γ ｓ γ ｓ γ ｇｄ ３
５ ０
式中：ｄ 、ｄ 分别为泥沙累积频率分布曲线上横坐标取值为 ３５％、５０％所对应的粒径值，ｍ；Ｊ为水
３５ ５０
３
面比降；ｇ为单宽输沙率，ｋｇ?ｓ。
ｂ
钱宁 ［２９］ 将经典推移质输沙公式统一转化为 Θ与 Φ 的关系，上述公式转化后的形式如下：
Ｍｅｙｅｒ － Ｐｅｔｅｒ式：
Φ＝ （４ Θ － ０．１８８） ３?２ （１１）
Ｅｎｇｅｌｕｎｄ式：

槡
槡
Φ＝ １１ ．６（ Θ － Θ ｃ ）（ Θ－ ０ ．７ Θ ｃ ） （１２）
Ａｃｋｅｒｓ － Ｗｈｉｔｅ式：
１６．５
Φ＝ ２ ．０２ｌｏｇ Ｊ Θ Θ（ Θ－ ０ ．１７） ３?２ （１３）
槡
( ) 槡
Ｔｓｕｂａｋｉ式：
０．６５
槡
Φ＝ ２５ （ ΘΘ ′） （ ΘΘ ′ － ０ ．８ Θ ｃ ） （１４）
— ４ １ —