Page 52 - 2024年第55卷第6期
P. 52
表 1 网格与时间步长收敛性验证
测试编号 网格数量 时间步长 C D 绝对误差 C L,rsm 绝对误差
1 87万 0.01 0.2807 0.1225
2 174 万 0.01 0.2765 0.0042 0.1120 0.0105
3 314 万 0.01 0.2729 0.0036 0.1080 0.0040
4 174 万 0.015 0.2822 0.1015
5 174万 0.01 0.2765 0.0057 0.1120 0.0105
6 174 万 0.005 0.2945 0.0180 0.1030 0.0091
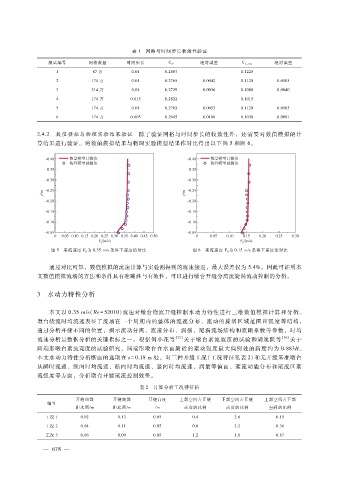
2.4.2 数值模拟与物理实验结果验证 除了验证网格与时间步长的收敛性外,还需要对数值模拟的计
算结果进行验证。将数值模拟结果与物理实验模型结果作对比得出以下图 5和图 6。
图 5 来流速度 V 0 为 0.35m?s条件下速度值对比 图 6 来流速度 V 0 为 0.15m?s条件下速度值对比
通过对比可知,数值模拟的流速计算与实验测得到的流速接近,最大误差仅为 5.4%。因此可证明本
文数值模拟流场的方法和条件具有准确性与有效性,可以进行墩台开缝分离流旋涡流动控制的分析。
3 水动力特性分析
本文以 0.35m?s(Re = 52010)流速对墩台绕流开缝控制水动力特性进行三维数值模拟计算和分析。
墩台绕流时均流速表征了流场在一个周期内的整体的流速分布、流动的旋涡区域范围和强度等结构,
通过分析开缝不同的位置,揭示流动分离、流速分布、涡强、尾涡流场结构和流阻系数等参数,时均
流速分析是数据分析的关键指标之一。根据何小花等 [25] 关于墩台紊流宽度的试验和胡旭跃等 [26] 关于
圆端形墩台紊流宽度的试验研究,圆端形墩台在水面附近的紊动强度最大值所处的高度约为 0.883H。
本文水动力特性分析断面的选取在 z = 0.18m处,对三种开缝工况(工况特征见表 2)和无开缝基准墩台
从瞬时流速、纵向时均流速、横向时均流速、竖向时均流速、涡量等值面、紊流动能分布和尾流区紊
流强度等方面,分析墩台开缝尾流控制效果。
表 2 计算分析工况特征值
开缝顶部 开缝底部 开缝高度 上部空间占开缝 下部空间占开缝 上部空间占下部
编号
距水面?m 距底面?m ?m 高度的比例 高度的比例 空间的比例
工况 1 0.02 0.13 0.05 0.4 2.6 0.15
工况 2 0.04 0.11 0.05 0.8 2.2 0.36
工况 3 0.06 0.09 0.05 1.2 1.8 0.67
— 6 7 —
8